Question

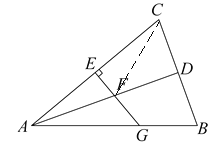
【题目】如图，在△ABC中，AB=AC，D是BC的中点，AC的垂直平分线分别交AC、AD、AB于点E、F、G.

(1)点F到△ABC的边_______的距离相等，点F到△ABC的顶点______的距离相等.

(2)若BC=6，AD=9，求AF的值.

(3)连接CG交AD于点H，当∠BAC是多少度时，△FGH为等腰三角形？

Answer 1

【答案】（1）AC，AB；A、B、C；（2）5；（3）45°或36°.

【解析】

（1）根据等腰三角形性质，AD平分∠BAC，AD垂直平分BC，F在AD上，根据角平分线性质解答；EF垂直平分AC，所以F为两边垂直平分线的交点．根据垂直平分线性质解答．

（2）连接FC,根据垂直平分线的性质得到AF=CF，设AF=x,则CF=x,DF=9-x,CD=BC=3,故利用Rt△FCD得到方程进行求解；

（3）根据△FGH为等腰三角形分三种情况分别讨论，根据垂直平分线与三角形的内角和即可求解.

（1）∵AB＝AC，D是BC的中点，

∴AD平分∠BAC，AD垂直平分BC．

∵点F在AD上，

∴点F到AC、AB的距离相等；

∵EF垂直平分AC，AD垂直平分BC．

∴FA＝FB＝FC，即点F到A、B、C的距离相等．

故答案为 AC、AB； A、B、C．

（2）连接FC,根据垂直平分线的性质得到AF=CF，

设AF=x,则CF=x,DF=9-x,CD=BC=3,

在Rt△FCD中，

即

解得x=5,

故AF=5；

（3）①当FG=HG时，故∠GFH=∠GHF,

∵∠GFH=∠EFA,∠EFA+∠EAF=90°，

同理∠CHD+∠HCD=90°

∴∠EAF =∠HCD,

∵AD垂直平分BC，

∴∠EAF =∠BAD,

∴∠HCD=∠BAD

∵AD⊥BC，∠B=∠B

∴CG⊥AB，

又EG垂直平分AC，

∴AG=CG，

故∠BAC=45°，

②当FH=HG时，故∠HFG=∠HGF,

∵∠GFH=∠EFA,∠EFA+∠EAF=90°，

又∠HGF+∠ECG=90°

∴∠EAF=∠ECG

∵EG垂直平分AC，∴∠ECG=∠EAG

∴此情况不存在；

③当FH=FG时，故∠FHG=∠FGH

∵∠FHG =∠CHD,∠CHD+∠HCD=90°，

又∠HGF+∠ECG=90°

∴∠EAF=∠ECG

∴∠ECG =∠HCD,

∵AD垂直平分BC，

∴∠ECG =∠BAC

设∠BAC=a，故∠ACG=∠HCD=a,∠ACB=2a，

∵AB=AC，∴∠ABC=∠ACB=2a

故∠BAC+∠ABC+∠ACB=5a=180°，

解得x=36°，

综上：∠BAC是45°或36°时，△FGH为等腰三角形.