题目内容
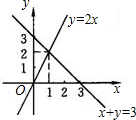 如下图所示,利用函数图象回答下列问题:
如下图所示,利用函数图象回答下列问题:(1)方程组
|
(2)不等式2x>-x+3的解集为
(3)不等式2x<-x+3的解集为
分析:(1)观察函数的图象y=2x与y=-x+3相交于点(1,2),从而求解;
(2)将不等式2x>-x+3,先移项,再系数化为1,从而求解;
(3)将不等式2x<-x+3,先移项,再系数化为1,从而求解;
(2)将不等式2x>-x+3,先移项,再系数化为1,从而求解;
(3)将不等式2x<-x+3,先移项,再系数化为1,从而求解;
解答:解:(1)观察图象可知,x+y=3与y=2x相交于(1,2).
可求出方程组的解为
.
故答案为:
.
(2)对不等式进行求解,
2x<-x+3可求得x>1,
故答案为:x>1.
(3)同理对不等式进行求解,
2x>-x+3可求得x<1,
故答案为:x<1.
可求出方程组的解为
|
故答案为:
|
(2)对不等式进行求解,
2x<-x+3可求得x>1,
故答案为:x>1.
(3)同理对不等式进行求解,
2x>-x+3可求得x<1,
故答案为:x<1.
点评:此题主要考查一次函数图形的性质,从图象入手解题较为简单.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
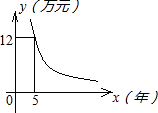 向银行付款y万元,预计x年后结清余款,y与x的函数关系如下图所示,试根据图象所提供的信息,回答下列问题:
向银行付款y万元,预计x年后结清余款,y与x的函数关系如下图所示,试根据图象所提供的信息,回答下列问题: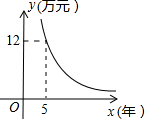 预计x年后结清余款,y与x的函数关系如下图所示,试根据图象所提供的信息,回答下列问题:
预计x年后结清余款,y与x的函数关系如下图所示,试根据图象所提供的信息,回答下列问题: 如下图所示,利用函数图象回答下列问题:
如下图所示,利用函数图象回答下列问题: 的解为______;
的解为______;