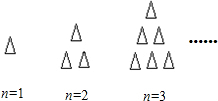题目内容
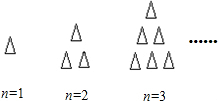 用火柴棒按上图的方式摆出一系列图案,按这种方式摆下去,第n个图案所用的火柴棒的根数为
用火柴棒按上图的方式摆出一系列图案,按这种方式摆下去,第n个图案所用的火柴棒的根数为| 3n2+3n |
| 2 |
| 3n2+3n |
| 2 |
分析:先根据图案排列规律求出第n个图案的三角形的个数,再根据没有个三角形有三根火柴棒计算即可得解.
解答:解:第1个图案有1个三角形,
第2个图案有1+2个三角形,
第3个图案有1+2+3个三角形,
…,
依此类推,第n个图案有:1+2+3+…+n个三角形,
∵1+2+3+…+n=
,
∴第n个图案所用的火柴棒的根数为3×
=
.
故答案为:
.
第2个图案有1+2个三角形,
第3个图案有1+2+3个三角形,
…,
依此类推,第n个图案有:1+2+3+…+n个三角形,
∵1+2+3+…+n=
| (1+n)n |
| 2 |
∴第n个图案所用的火柴棒的根数为3×
| (1+n)n |
| 2 |
| 3n2+3n |
| 2 |
故答案为:
| 3n2+3n |
| 2 |
点评:本题是对图形变化规律的考查,先求出第n个图案的三角形的个数是解题的关键.

练习册系列答案
相关题目
如图所示,是一列用若干根火柴棒摆成的由正方形组成的图案.
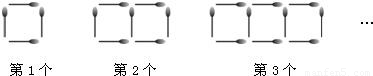
(1)完成下表的填空:
(2)某同学用若干根火柴棒按如上图列的方式摆图案,摆完了第1个后,摆第2个,接着摆第3个,第4个,…,当他摆完第n个图案时剩下了20根火柴棒,要刚好摆完第n+1个图案还差2根.问最后摆的图案是第几个图案?

(1)完成下表的填空:
| 正方形个数 | 1 | 2 | 3 | 4 | 5 | 6 | n |
| 火柴棒根数 | 4 | 7 | 10 | 13 |
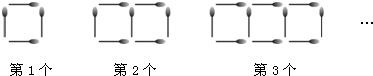

 用火柴棒按上图的方式摆出一系列图案,按这种方式摆下去,第n个图案所用的火柴棒的根数为________.
用火柴棒按上图的方式摆出一系列图案,按这种方式摆下去,第n个图案所用的火柴棒的根数为________.