Question

【题目】 定义：两组邻边分别相等的四边形叫做筝形.

(1)、请写出除定义外的性质和判定猜想各一条，并从定义出发证明你的判定猜想.

(2)、筝型ABCD中,对角线AC,BD相交于点O.

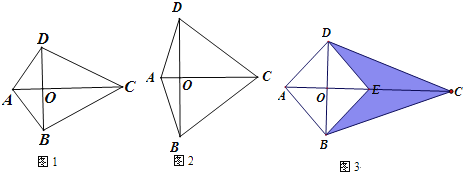
①如图1,若BD=CO,求tan∠BCD的值.

②如图2,若∠DAC=∠BCD=72,求AD:CD的值.

(3)、如图3，把△ABD沿着对角线BD翻折，A点落在对角线AC上的E点．如果△AOD中，一个内角是另一个内角的2倍，且阴影部分图形的面积等于四边形ABED的面积，直接写出的值.

Answer 1

【答案】(1)、答案见解析；(2)、tan∠BCD=；；(3)、1:或1:或1:.

【解析】

试题分析：(1)、利用三角全等来进行证明；(2)、设OC=2OD=2OB=a，则CD=BD=a，根据△BCD的面积得出sin∠BCD的值，从而得到tan∠BCD的值；(3)、作∠BCD的平分线交AC于点E，根据题意得出∠2=36°，从而得出△DAE∽△CDA，从而得出，得出比值；根据题意直接得出比值.

试题解析：(1)、性质：①筝形有一组对角相等；

判定：①有一条对角线垂直平分另一条对角线的四边形是筝形；

(2)、①、设OC=2OD=2OB=a,则CD=BD=a,

∵CDCBsin∠BCD=BDCO ∴sin∠BCD=×2a×2a

可得：sin∠BCD=,即：tan∠BCD=.

②、作∠BCD的平分线交AC于点E.

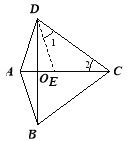
∵∠BCD=72，∴∠2=∠BCD=36∵∠DAC=72，

∴∠ADC=72，∠1=36 ∴△DAE∽△CDA ∴, DC=AC,AE=AC-CE=CD-AD

即：，去分母得：AD2+CDAD-CD2=0，解得AD=CD，AD=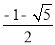CD（舍去），∴AD:CD=

(3)、1:或1:或1:.