��Ŀ����
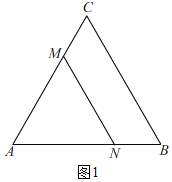
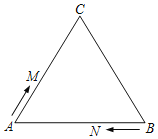
����Ŀ����ͼ���ȱ���ABC�ı߳�Ϊ15cm����������M��N�ֱ�ӵ�A����Bͬʱ�������������εı�˳ʱ���˶�����֪��M���ٶ�Ϊ1cm/s����N���ٶ�Ϊ2cm/s������N��һ�ε���B��ʱ��M��Nͬʱֹͣ�˶�
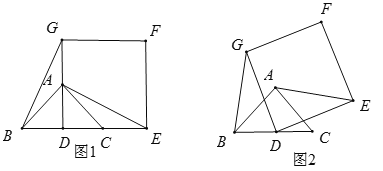
��1����M��N�˶������M��N�����غϣ�
��2����M��N�˶��������AMNΪ�ȱ������Σ�
��3������M��N��BC�����˶�ʱ���ܷ�õ���MNΪ�ױߵĵ���������AMN������ڣ��������ʱM��N�˶���ʱ�䣮
���𰸡���1��15�룻��2��5�룻��3��20��
��������
��1���ɵ�N�˶�·�̣���M�˶�·��+AB���·�̣��г�������⣬�ݿ˵ó����ۣ�
��2���ɵȱ������ε����ʿɵ�AN��AM�����з�����⣬���ɵó����ۣ�
��3����ȫ�������ε����ʿɵ�CM��BN�����з�����⣬���ɵó����ۣ�
��1�����˶�t�룬M��N�����غϣ�
��������ã�2t��t��15��
��t��15��
�𣺵�M��N�˶�15���M��N�����غϣ�
��2����ͼ1�����M��N�˶�x�����AMNΪ�ȱ������Σ�
��AN��AM��
���˶�֪��AN��15��2x��AM��x��
��15��2x��x��
��ã�x��5��
����M��N�˶�5�����AMN�ǵȱ������Σ�
��3��������ڣ�
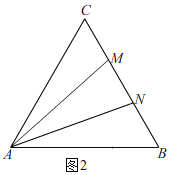
��ͼ2����M��N�˶�y��õ���MNΪ�ױߵĵ���������AMN��
��AM��AN��
���AMN����ANM��
�ߡ�ABC�ǵȱ������Σ�
��AB��AC����C����B��60����
���ACN�ա�ABM��AAS����
��CN��BM��
��CM��BN��
���˶�֪��CM��y��15��BN��15��3��2y��
��y��15��15��3��2y��
��y��20��
�ʵ�M��N��BC�����˶�ʱ���ܵõ���MNΪ�ױߵĵ���������AMN����ʱM��N�˶���ʱ��Ϊ20�룮