题目内容
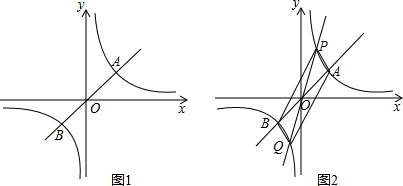
如图(1)所示,正比例函数y=kx与反比例函数y=
的图象交于点A(-3,2).

(1)试确定上述正比例函数与反比例函数的解析式;
(2)根据图象回答,在第二象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)如图(2)所示,P(m,n)是反比例函数图象上的一动点,其中-3<m<0,过点P作直线PB∥x轴,交y轴于点B,过点A作直线AD∥y轴,交x轴于点D,交直线PB于点C.当四边形OACP的面积为6时,请判断线段BP与CP的大小关系,并说明理由.
(4)在第(3)问条件中,连接AP,若∠PAO=90°,试求分式m2+
的值.
| t |
| x |

(1)试确定上述正比例函数与反比例函数的解析式;
(2)根据图象回答,在第二象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)如图(2)所示,P(m,n)是反比例函数图象上的一动点,其中-3<m<0,过点P作直线PB∥x轴,交y轴于点B,过点A作直线AD∥y轴,交x轴于点D,交直线PB于点C.当四边形OACP的面积为6时,请判断线段BP与CP的大小关系,并说明理由.
(4)在第(3)问条件中,连接AP,若∠PAO=90°,试求分式m2+
| 16 |
| m2 |
(1)把A(-3,2)代入y=kx得:2=-3k,
解得:k=-
,
∴y=-
x,
代入y=
得:t=-6,
∴y=-
.
答:正比例函数与反比例函数的解析式分别是y=-
x,y=-
.
(2)∵A(-3,2),
由图象可知:当-3<x<0时,在第二象限内,反比例函数的值大于正比例函数的值.
(3)答:线段BP与CP的大小关系是BP=CP,
理由是:∵P(m,n)在y=-
上,
∴mn=-6,
∵DO=3,AD=2,OB=n,BP=-m,CP=3-PB,DC=n,
四边形OACP的面积为6,
∴S矩形CDOB-S△ADO-S△OBP=6,
3n-
×3×2-
×(-mn)=6,
3n-3-
×6=6,
3n=12,
解得:n=4,
∴m=-
=-
,
∴P(-
,4),
∴PB=
,CP=3-
=
,
∴BP=CP.
(4) ∵P(m,n),P点在y=-
∵P(m,n),P点在y=-
图象上,
∴mn=-6,
∴n=-
,
∵∠PAO=90°,
∴∠CAP+∠DAO=90°,
∵∠AOD+∠DAO=90°,
∴∠AOD=∠CAP,
又∵∠C=∠ADO=90°,
∴△CAP∽△DOA,
∴
=
,
∴
=
,
解得:m1=-3(不合题意舍去),m2=-
,
∴m2+
=(-
)2+
=
.
解得:k=-
| 2 |
| 3 |
∴y=-
| 2 |
| 3 |
代入y=
| t |
| x |
∴y=-
| 6 |
| x |
答:正比例函数与反比例函数的解析式分别是y=-
| 2 |
| 3 |
| 6 |
| x |
(2)∵A(-3,2),
由图象可知:当-3<x<0时,在第二象限内,反比例函数的值大于正比例函数的值.
(3)答:线段BP与CP的大小关系是BP=CP,
理由是:∵P(m,n)在y=-
| 6 |
| x |
∴mn=-6,
∵DO=3,AD=2,OB=n,BP=-m,CP=3-PB,DC=n,
四边形OACP的面积为6,
∴S矩形CDOB-S△ADO-S△OBP=6,
3n-
| 1 |
| 2 |
| 1 |
| 2 |
3n-3-
| 1 |
| 2 |
3n=12,
解得:n=4,
∴m=-
| 6 |
| 4 |
| 3 |
| 2 |
∴P(-
| 3 |
| 2 |
∴PB=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴BP=CP.
(4)
 ∵P(m,n),P点在y=-
∵P(m,n),P点在y=-| 6 |
| x |
∴mn=-6,
∴n=-
| 6 |
| m |
∵∠PAO=90°,
∴∠CAP+∠DAO=90°,
∵∠AOD+∠DAO=90°,
∴∠AOD=∠CAP,
又∵∠C=∠ADO=90°,
∴△CAP∽△DOA,
∴
| AD |
| CP |
| DO |
| AC |
∴
| 2 |
| 3+m |
| 3 | ||
-
|
解得:m1=-3(不合题意舍去),m2=-
| 4 |
| 3 |
∴m2+
| 16 |
| m2 |
| 4 |
| 3 |
| 16 | ||
(-
|
| 97 |
| 9 |

练习册系列答案
相关题目