题目内容
【题目】已知二次函数![]() (k>0).
(k>0).
(1)当k=![]() 时,求这个二次函数的顶点坐标;
时,求这个二次函数的顶点坐标;
(2)求证:关于x的一元次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
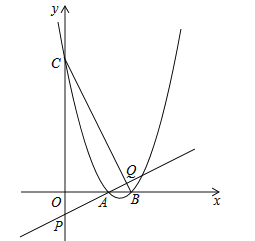
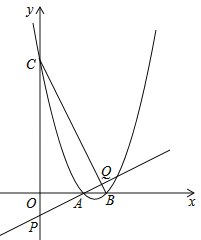
(3)如图,该二次函数与x轴交于A、B两点(A点在B点的左侧),与y轴交于C点,P是y轴负半轴上一点,且OP=1,直线AP交BC于点Q,求证:![]() .
.
【答案】(1)(1,![]() );(2)证明见解析;(3)证明见解析.
);(2)证明见解析;(3)证明见解析.
【解析】
试题分析:(1)直接将k的值代入函数解析式,进而利用配方法求出顶点坐标;
(2)利用根的判别式得出△=1,进而得出答案;
(3)根据题意首先表示出Q点坐标,以及表示出OA,AB的长,再利用两点之间距离求出AQ的长,进而求出答案.
试题解析:(1)将k=![]() 代入二次函数可求得,
代入二次函数可求得,![]() =
=![]() ,故抛物线的顶点坐标为:(1,
,故抛物线的顶点坐标为:(1,![]() );
);
(2)∵一元次方程![]() ,∴△=
,∴△=![]() =
=![]() =1>0,∴关于x的一元次方程
=1>0,∴关于x的一元次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
(3)由题意可得:点P的坐标为(0,1),则![]() ,(x﹣k﹣1)(x﹣k)=0,故A(k,0),B(k+1,0),当x=0,则y=
,(x﹣k﹣1)(x﹣k)=0,故A(k,0),B(k+1,0),当x=0,则y=![]() ,故C(0,
,故C(0,![]() ),则AB=k+1﹣k=1,OA=k,可得:
),则AB=k+1﹣k=1,OA=k,可得:![]() =
=![]() ,
,![]() =
=![]() ,当
,当![]() =
=![]() ,解得:x=
,解得:x=![]() ,则代入原式可得:y=
,则代入原式可得:y=![]() ,则点Q坐标为(
,则点Q坐标为(![]() ,
,![]() ).运用距离公式得:
).运用距离公式得:![]() =
=![]() =
=![]() ,则
,则![]() ,
,![]() =1,故
=1,故![]() =
=![]() =
=![]() =
=![]() ,则
,则![]() .
.

练习册系列答案
相关题目