题目内容
(2006•黄石)金华商店门前和店内MP4柜台前分别横排着6块灯箱广告牌,现决定在这两排广告牌中共拆除8块,以增加顾客流通量,已知进入店内顾客流通增加量与前排广告牌拆除块数成正比,MP4柜台顾客流通增加量和店内顾客流通增加量与柜前广告牌拆除块数之积成正比,要使MP4柜台顾客流通增加量最大,则前后两排各拆除广告牌 块.
【答案】分析:设商店门前广告牌拆除块数为x,则柜前广告牌拆除块数(8-x).需根据进入店内顾客流通增加量与前排广告牌拆除块数成正比,得到x与k1之间的关系式;然后根据MP4柜台顾客流通增加量和店内顾客流通增加量与柜前广告牌拆除块数之积成正比,得到一个二次函数.从而运用公式求最值,即可解答.
解答:解:设商店门前广告牌拆除块数为x,则柜前广告牌拆除块数(8-x).
由进入店内顾客流通增加量与前排广告牌拆除块数成正比;
设y1=k1x;
由MP4柜台顾客流通增加量和店内顾客流通增加量与柜前广告牌拆除块数之积成正比,
设y2=k2y1(8-x)=k1k2x(8-x)=-k1k2x2+8k1k2x,(其中k1,k2是常数,且不为0)
由二次函数性质,
当x=-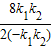 =4时,柜台顾客流通增加量y2最大,
=4时,柜台顾客流通增加量y2最大,
此时8-x=4.
点评:本题考查二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.
解答:解:设商店门前广告牌拆除块数为x,则柜前广告牌拆除块数(8-x).
由进入店内顾客流通增加量与前排广告牌拆除块数成正比;
设y1=k1x;
由MP4柜台顾客流通增加量和店内顾客流通增加量与柜前广告牌拆除块数之积成正比,
设y2=k2y1(8-x)=k1k2x(8-x)=-k1k2x2+8k1k2x,(其中k1,k2是常数,且不为0)
由二次函数性质,
当x=-
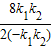 =4时,柜台顾客流通增加量y2最大,
=4时,柜台顾客流通增加量y2最大,此时8-x=4.
点评:本题考查二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(2006•黄石)学生李杨从家里到学校只能乘106路或108路公共汽车,他对这两路车途中所需时间分别做了14次统计,并列成下表:
106路
108路
(1)若李杨每天早上6点25分上车,学校7点10分上课,则请你根据统计知识为李杨选择合理的一路车;
(2)若李杨每天早上6点25分上车,学校7点上课,则乘哪路车合适并说明理由;
(3)若在(2)中选择了A路车,已知A路车仅有车况等级为上、中、下的3辆车,李杨采取的策略是:放过第一辆,若第二辆比第一辆好,则乘第二辆,否则乘第三辆.在不考虑时间的情况下,李杨乘上等车的频率有多大?
106路
| 时间(分) | 20 | 25 | 30 | 35 | 40 | 45 |
| 次数 | 1 | 1 | 3 | 6 | 1 | 2 |
| 时间(分) | 20 | 25 | 30 | 35 | 40 | 45 |
| 次数 | 2 | 1 | 3 | 4 | 3 | 1 |
(2)若李杨每天早上6点25分上车,学校7点上课,则乘哪路车合适并说明理由;
(3)若在(2)中选择了A路车,已知A路车仅有车况等级为上、中、下的3辆车,李杨采取的策略是:放过第一辆,若第二辆比第一辆好,则乘第二辆,否则乘第三辆.在不考虑时间的情况下,李杨乘上等车的频率有多大?


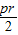 知一个多边形周长为p,若内切圆半径为r,则其面积等于
知一个多边形周长为p,若内切圆半径为r,则其面积等于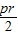 .
.