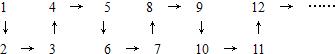题目内容
将正整数按以下规律排列,则2008所在的位置是第________行第________列
第一列 第二列 第三列 第四列 …
第一行 1 2 9 10 …
第二行 4 3 8 11 …
第三行 5 6 7 12 …
第四行 16 15 14 13 …
第五行 17 …
…
18 45
分析:通过观察图中数字的排列,可知偶数行的第一列为4、16…相邻偶数的平方,而且后面的数则依次加1,第n列就加(n-1)个1,再拐弯加1;奇数列的第一行数为1、9…相邻奇数的平方,而且向下依次减1,第n行就减(n-1)个1,再拐弯减1.
解答:∵2008=442+72,442=1936,
则从1937开始从第45行开始数,到第45列1980开始拐弯,到第18行就是2008,
则2008所在的位置是第18行第45列.
故答案为:18,45.
点评:考查了规律型:数字的变化,本题还可以这样解答,横着看,偶数行的第一个数刚好是行数的平方,从列看是奇数列的第一个数刚好是列数的平方.452=2025,2025是第45列第一个数,奇数列从上往下前几个数(几个,刚好是列数)是顺序减少的,所以2025可以往下减少45个数,而2008仅仅比2025少17,所以他是在45列第18行.
分析:通过观察图中数字的排列,可知偶数行的第一列为4、16…相邻偶数的平方,而且后面的数则依次加1,第n列就加(n-1)个1,再拐弯加1;奇数列的第一行数为1、9…相邻奇数的平方,而且向下依次减1,第n行就减(n-1)个1,再拐弯减1.
解答:∵2008=442+72,442=1936,
则从1937开始从第45行开始数,到第45列1980开始拐弯,到第18行就是2008,
则2008所在的位置是第18行第45列.
故答案为:18,45.
点评:考查了规律型:数字的变化,本题还可以这样解答,横着看,偶数行的第一个数刚好是行数的平方,从列看是奇数列的第一个数刚好是列数的平方.452=2025,2025是第45列第一个数,奇数列从上往下前几个数(几个,刚好是列数)是顺序减少的,所以2025可以往下减少45个数,而2008仅仅比2025少17,所以他是在45列第18行.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将正整数依次按下表规律排成四列:
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 2 | 3 | |
| 第2行 | 6 | 5 | 4 | |
| 第3行 | 7 | 8 | 9 | |
| 第4行 | 12 | 11 | 10 | |
| … |
(1)数23的位置应排在第______行第______列;
(2)数2010的位置应排在第______行第______列;
(3)如果用图中这样的十字框框出表中的5个数(如:6,7,8,9,12),设中间的数为x,请用代数式分别表示其余的四个数;

(4)在(3)中的五个数的和能等于6012吗?能等于9017吗?若能,分别求出这五个数;若不能,请说明理由.