题目内容
如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
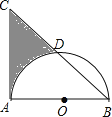
A.24﹣4π B.32﹣4π C.32﹣8π D.16
练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
题目内容
如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )

A.24﹣4π B.32﹣4π C.32﹣8π D.16
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案