题目内容
一元二次方程8x2-(m-1)x+m-7=0,
(1)m为何实数时,方程的两个根互为相反数?
(2)m为何实数时,方程的一个根为零?
(3)是否存在实数m,使方程的两个根互为倒数?
(1)m为何实数时,方程的两个根互为相反数?
(2)m为何实数时,方程的一个根为零?
(3)是否存在实数m,使方程的两个根互为倒数?
分析:(1)当方程的两个根互为相反数时,x1+x2=
=0,通过解此方程可以求得m的值;
(2)当方程的一根是零时,由根与系数的关系知x1•x2=0,据此列出关于m的方程,通过解方程即可求得m的值;
(3)当方程的两个根互为倒数时,由根与系数的关系知x1•x2=1,据此列出关于m的方程,通过解方程即可求得m的值;然后通过根的判别式进行判断是否存在这样的实数m.
| m-1 |
| 8 |
(2)当方程的一根是零时,由根与系数的关系知x1•x2=0,据此列出关于m的方程,通过解方程即可求得m的值;
(3)当方程的两个根互为倒数时,由根与系数的关系知x1•x2=1,据此列出关于m的方程,通过解方程即可求得m的值;然后通过根的判别式进行判断是否存在这样的实数m.
解答:解:(1)∵一元二次方程8x2-(m-1)x+m-7=0的两个根互为相反数,
∴x1+x2=
=0,
解得m=1;
(2)∵一元二次方程8x2-(m-1)x+m-7=0的一个根为零,
∴x1•x2=
=0,
解得m=7;
(3)设存在实数m,使方程8x2-(m-1)x+m-7=0的两个根互为倒数,则
x1•x2=
=1,
解得m=15;
则原方程为4x2-7x+4=0,
△=49-4×4×4=-15<0,所以原方程无解,这与存在实数m,使方程8x2-(m-1)x+m-7=0有两个根相矛盾.故不存在这样的实数m.
∴x1+x2=
| m-1 |
| 8 |
解得m=1;
(2)∵一元二次方程8x2-(m-1)x+m-7=0的一个根为零,
∴x1•x2=
| m-7 |
| 8 |
解得m=7;
(3)设存在实数m,使方程8x2-(m-1)x+m-7=0的两个根互为倒数,则
x1•x2=
| m-7 |
| 8 |
解得m=15;
则原方程为4x2-7x+4=0,
△=49-4×4×4=-15<0,所以原方程无解,这与存在实数m,使方程8x2-(m-1)x+m-7=0有两个根相矛盾.故不存在这样的实数m.
点评:本题综合考查了根与系数的关系、倒数与相反数的定义以及根的判别式.一元二次方程8x2-(m-1)x+m-7=0的m的取值受根的判别式的符号的限制.

练习册系列答案
相关题目
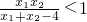 ,则实数m取值范围是______;
,则实数m取值范围是______;