��Ŀ����
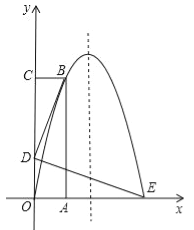
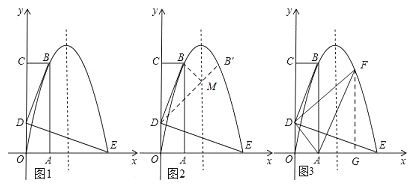
����Ŀ����ͼ��������OABC��OA����x����������ϣ�OC��y����������ϣ�������y=ax2+bx������B��1��4���͵�E��3��0�����㣮
��1���������ߵĽ���ʽ��
��2������D���߶�OC�ϣ���BD��DE��BD=DE����D������ꣻ
��3����������2���£��������ߵĶԳ�������һ��M��ʹ�á�BDM���ܳ�Ϊ��С�������BDM�ܳ�����Сֵ����ʱ��M�����ꣻ
��4����������2���£���B�㵽E����������ߵ�ͼ���ϣ��Ƿ����һ����P��ʹ�á�PAD�������������ڣ��������PAD��������ֵ����ʱP������ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=��2x2+6x����2��D��0��1������3����BDM���ܳ���СֵΪ![]() ��M��
��M��![]() ��
��![]() ������4����P��������
������4����P��������![]() ��
��![]() ����
����
��������
�����������1������B��1��4����E��3��0����������������ߵĽ���ʽ���õ�����a��b�ķ����飬���a��b��ֵ���Ӷ��ɵõ������ߵĽ���ʽ����2������ͬ�ǵ�������֤����BDC=��DE0��Ȼ��������AAS֤����BDC�ա�DEO���Ӷ��õ�OD=AO=1�����ǿ���õ�D�����ꣻ��3������B���������ߵĶԳ���ĶԳƵ�B��������B��D�������ߵĶԳ������M������������ߵĶԳ��᷽�̣��Ӷ��õ���B�������꣬����ԳƵ����ʿ�֪����D��M��B����һ��ֱ����ʱ����BMD���ܳ�����Сֵ�����������ľ��빫ʽ���BD��B��D�ij��ȣ��Ӷ��õ������ε��ܳ���Сֵ��Ȼ�����ݴ���ϵ�������D��B���Ľ���ʽ��Ȼ��M�ĺ�����������õ�M�������ꣻ��4������F��FG��x�ᣬ����ΪG�����F��a����2a2+6a������OG=a��FG=��2a2+6a��Ȼ������S��FDA=S����DOGF��S��ODA��S��AGF�������ε������a�ĺ�����ϵʽ��Ȼ�����ݶ��κ�����������⼴�ɣ�
�����������1������B��1��4����E��3��0����������������ߵĽ���ʽ�ã�![]() ��
��
��ã�a=-2��b=6��
�����ߵĽ���ʽΪy=��2x2+6x��
��2����ͼ1��ʾ��
��BD��DE��
���BDE=90����
���BDC+��EDO=90����
���ߡ�ODE+��DEO=90����
���BDC=��DE0��
����BDC����DOE��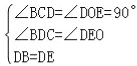 ��
��
���BDC�ա�DEO��
��OD=AO=1��
��D��0��1����
��3����ͼ2��ʾ������B���������ߵĶԳ���ĶԳƵ�B��������B��D�������ߵĶԳ������M��
��x=��![]() =
=![]() ��
��
����B����������2��4����
����B���B������x=![]() �Գƣ�
�Գƣ�
��MB=B��M��
��DM+MB=DM+MB����
������D��M��B����һ��ֱ����ʱ��MD+MB����Сֵ������BMD���ܳ�����Сֵ����
���������ľ��빫ʽ��֪��BD=![]() ��DB��=
��DB��=![]() ��
��
���BDM����Сֵ=![]() ��
��
��ֱ��B��D�Ľ���ʽΪy=kx+b��
����D��B�����������ã�![]() ��
��
��ã�k=![]() ��b=1��
��b=1��
��ֱ��DB���Ľ���ʽΪy=![]() x+1��
x+1��
��x=![]() ����ã�y=
����ã�y=![]() ��
��
��M��![]() ��
��![]() ����
����
��4����ͼ3��ʾ������F��FG��x�ᣬ����ΪG��
���F��a����2a2+6a������OG=a��FG=��2a2+6a��
��S����DOGF=![]() ��OD+FG��OG=
��OD+FG��OG=![]() ����2a2+6a+1����a=��a3+3a2+
����2a2+6a+1����a=��a3+3a2+![]() a��S��ODA=
a��S��ODA=![]() ODOA=
ODOA=![]() ��1��1=
��1��1=![]() ��S��AGF=
��S��AGF=![]() AGFG=��a3+4a2��3a��
AGFG=��a3+4a2��3a��
��S��FDA=S����DOGF��S��ODA��S��AGF=��a2+![]() a��
a��![]() ��
��
����a=![]() ʱ��S��FDA�����ֵΪ
ʱ��S��FDA�����ֵΪ![]() ��
��
����P��������![]() ��
��![]() ����
����

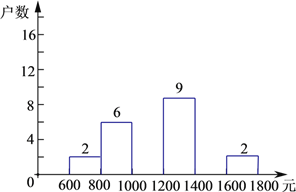
����Ŀ��С����ѧУ��֯���������и����˽�������ס��С��560������ļ�ͥ������������������������һ�������ļ�ͥ�������������ȡ��������λ��Ԫ���������������µ�Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
���� | Ƶ�� | �ٷֱ� |
600��x��800 | 2 | 5% |
800��x��1000 | 6 | 15% |
1000��x��1200 | a | 40% |
1200��x��1400 | 9 | 22.5% |
1400��x��1600 | b | c |
1600��x��1800 | 2 | 5% |
�ϼ� | 40 | 100% |
���������ṩ����Ϣ������������⣺
��1��Ƶ���ֲ����У�a= ��b= ��c= ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3������Ƹþ���С����ͥ�����е����루����1000����1600Ԫ���Ĵ�Լ�ж��ٻ���