题目内容
【题目】如图(1),AB=4cm,AC⊥AB于A,BD⊥AB于B,AC=BD=3cm.点P在线段AB上以lcm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).

(1)若点Q的运动速度与点P的运动速度相等,当t=l时,△ACP与△BPQ是否全等?PC与PQ是否垂直?请分别说明理由;
(2)如图(2),将图(1)中的“AC上AB于A,BD上AB于B”改为“∠CAB=∠DBA=60![]() ”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
【答案】(1) △ACP≌△BPQ,PC垂直于PQ,理由见解析.(2)存在,见解析.
【解析】试题分析:(1)利用SAS证得△ACP≌△BPQ,得出∠ACP=∠BPQ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可;
(2)由△ACP≌△BPQ,分两种情况:①AC=BP,AP=BQ,②AC=BQ,AP=BP,建立方程组求得答案即可.
试题解析:(1)当t=1时,△ACP≌△BPQ,PC垂直于PQ
理由如下:
当t=1时,AP=BQ=1,BP=AC=3,
又∠A=∠B=90°,
∴在△ACP和△BPQ中,
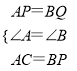
∴△ACP≌△BPQ.
∴∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°.
∴∠CPQ=90°,即线段PC与线段PQ垂直.
(2)①若△ACP≌△BPQ,
则AC=BP,AP=BQ,
![]()
解得![]()
②若△ACP≌△BQP,
则AC=BQ,AP=BP,
![]() 解得
解得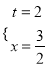
综上所述,存在![]() 或
或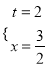 使得△ACP与△BPQ全等.
使得△ACP与△BPQ全等.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目


