题目内容
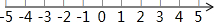 如图是一条数轴,请你结合数轴与绝对值的知识回答下列问题:
如图是一条数轴,请你结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示-4和2的两点之间的距离是______;
(2)一般地,数轴上表示数m和数n的两点之间的距离等于|m-n|,如果表示数a和-1的两点之间的距离是4,则a的值是______;
(3)若数轴上表示数a的点位于-3与1之间,则化简|a+3|+|a-1|的结果是______;
(4)当a=______时,|a+3|+|a-2|+|a-4|的值最小,最小值是______.
解:(1)数轴上表示-4和2的两点之间的距离是6;
故答案为:6;
(2)|a-(-1)|=4,
|a+1|=4,
a+1=4,a+1=-4,
解得:a=3或-5;
故答案为:3或-5;
(3)∵数a的点位于-3与1之间,
∴a+3>0,a-1<0,
∴|a+3|+|a-1|=a+3+(-a+1)=a+3-a+1=4;
故答案为:4;
(4)a=2有最小值,最小值=|2+3|+|2-2|+|2-4|=5+0+2=7.
故答案为:2,7.
分析:(1)根据数轴,求出两个数的差的绝对值即可;
(2)根据两点间的距离的表示列式计算即可得解;
(3)先去掉绝对值号,然后进行计算即可得解;
(4)判断出a=2时,三个绝对值的和最小,然后进行计算即可得解.
点评:本题考查了绝对值,数轴,读懂题目信息,理解数轴上两个数之间的距离的表示方法是解题的关键.
故答案为:6;
(2)|a-(-1)|=4,
|a+1|=4,
a+1=4,a+1=-4,
解得:a=3或-5;
故答案为:3或-5;
(3)∵数a的点位于-3与1之间,
∴a+3>0,a-1<0,
∴|a+3|+|a-1|=a+3+(-a+1)=a+3-a+1=4;
故答案为:4;
(4)a=2有最小值,最小值=|2+3|+|2-2|+|2-4|=5+0+2=7.
故答案为:2,7.
分析:(1)根据数轴,求出两个数的差的绝对值即可;
(2)根据两点间的距离的表示列式计算即可得解;
(3)先去掉绝对值号,然后进行计算即可得解;
(4)判断出a=2时,三个绝对值的和最小,然后进行计算即可得解.
点评:本题考查了绝对值,数轴,读懂题目信息,理解数轴上两个数之间的距离的表示方法是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目

 如图是一条数轴,请你结合数轴与绝对值的知识回答下列问题:
如图是一条数轴,请你结合数轴与绝对值的知识回答下列问题:
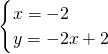 的解.
的解.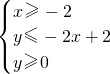 ,所围成的区域.
,所围成的区域.

 的解.
的解. ,所围成的区域.
,所围成的区域.