题目内容
若反比例函数y=-
的图象上有两点A(1,y1),B(2,y2),则y1 y2.(填“>”,“=”或“<”)
| 2 |
| x |
考点:反比例函数图象上点的坐标特征
专题:
分析:直接把两点A(1,y1),B(2,y2)代入反比例函数求出y1,y2的值,并比较出其大小即可.
解答:解:∵点A(1,y1),B(2,y2)在反比例函数y=-
的图象上,
∴y1=-
=-2,y2=-
=-1,
∵-2<-1,
∴y1<y2.
故答案为:<.
| 2 |
| x |
∴y1=-
| 2 |
| 1 |
| 2 |
| 2 |
∵-2<-1,
∴y1<y2.
故答案为:<.
点评:本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
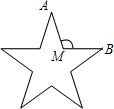 如图,五角星的五个角都是顶角为36°的等腰三角形,为了画出这个五角星,还需要知道∠AMB的度数,那么∠AMB的度数为( )
如图,五角星的五个角都是顶角为36°的等腰三角形,为了画出这个五角星,还需要知道∠AMB的度数,那么∠AMB的度数为( )| A、108° | B、120° |
| C、136° | D、144° |
 反比例函数y=
反比例函数y=| k |
| x |
| A、①②③④ | B、①②③ |
| C、①②④ | D、②③④ |
下列车标图案中,是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.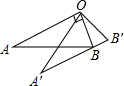 如图,∠AOB=90°,将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′,使点B恰好落在边A′B′上.已知tanA=
如图,∠AOB=90°,将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′,使点B恰好落在边A′B′上.已知tanA=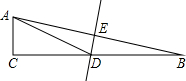 如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC与D,交AB于E.若BD=12,则AC=
如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC与D,交AB于E.若BD=12,则AC= 如图,热气球的探测器显示,从热气球点A处看我市一栋高楼顶部B点处的仰角为60°,看这栋高楼底部C点处的俯角为30°,热气球与高楼的水平距离为66m,求这栋高楼的高度.(结果精确到0.1m,参考数据:
如图,热气球的探测器显示,从热气球点A处看我市一栋高楼顶部B点处的仰角为60°,看这栋高楼底部C点处的俯角为30°,热气球与高楼的水平距离为66m,求这栋高楼的高度.(结果精确到0.1m,参考数据: