题目内容
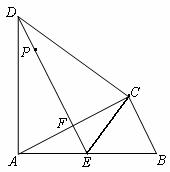
如图，△ABC中，∠ACB＝90°，以AC为边在△ABC外作等边三角形ACD，过点D作AC的垂线，垂足为F，与AB相交于点E，连接CE。
(1)说明：AE=CE=BE；
(2)若AB＝15 cm， P是直线DE上的一点。则当P在何处时， PB+PC最小，并求出此时PB+PC的值。
（1）等边三角形ADC中，∵DF⊥AC, ∴DF垂直平分AC, ∴AE=CE ;（2分）
∴∠ACE=∠CAE，∵∠ACB=90°，∴∠ACE+∠BCE=∠CAE+∠B=90°, ∴∠BCE=∠B, （2分）
∴CE=BE,∴AE=CE=BE。（2分）
（2）∵DE垂直平分AC，∴PC=PA，∴PB+PC= PB +PA；
练习册系列答案
相关题目
26、已知：如图，△ABC中，点D在AC的延长线上，CE是∠DCB的角平分线，且CE∥AB．
27、已知：如图，△ABC中，∠BAC=60°，D、E两点在直线BC上，连接AD、AE．
27、如图，△ABC中，AD⊥BC于D，DN⊥AC于N，DM⊥AB于M
14、如图，△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C的大小是（ ）
已知，如图，△ABC中，点D在BC上，且∠1=∠C，∠2=2∠3，∠BAC=70°．