题目内容
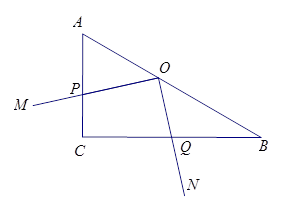
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上, OM、ON分别交CA、CB于点P、Q,∠MON绕点O任意旋转.当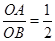 时,
时, 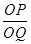 的值为 ;当
的值为 ;当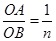 时,
时,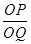 的值为 .(用含n的式子表示)
的值为 .(用含n的式子表示)
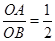 时,
时, 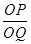 的值为 ;当
的值为 ;当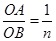 时,
时,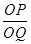 的值为 .(用含n的式子表示)
的值为 .(用含n的式子表示)

如图,过点O作OH⊥AC于H,OG⊥BC于G,由条件可以表示出HO、GO的值,通过证明△PHO∽△QGO由相似三角形的性质就可以求出结论.
解答: 解:过点O作OH⊥AC于H,OG⊥BC于G,
解:过点O作OH⊥AC于H,OG⊥BC于G,
∴∠OHP=∠OGQ=90°.
∵∠ACB=90°,
∴四边形HCGO为矩形,
∴∠HOG=90°,
∴∠HOP=∠GOQ,
∴△PHO∽△QGO,
∴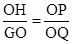 .
.
∵ ,设OA=x,则OB=2x,且∠ABC=30°,
,设OA=x,则OB=2x,且∠ABC=30°,
∴AH= x,OG=x.
x,OG=x.
在Rt△AHO中,由勾股定理,得
OH= x,
x,
∴ ,
,
∴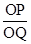 =
= .
.
故答案为: .
.
解答:
 解:过点O作OH⊥AC于H,OG⊥BC于G,
解:过点O作OH⊥AC于H,OG⊥BC于G,∴∠OHP=∠OGQ=90°.
∵∠ACB=90°,
∴四边形HCGO为矩形,
∴∠HOG=90°,
∴∠HOP=∠GOQ,
∴△PHO∽△QGO,
∴
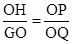 .
.∵
 ,设OA=x,则OB=2x,且∠ABC=30°,
,设OA=x,则OB=2x,且∠ABC=30°,∴AH=
 x,OG=x.
x,OG=x.在Rt△AHO中,由勾股定理,得
OH=
 x,
x,∴
 ,
,∴
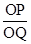 =
= .
.故答案为:
 .
.
练习册系列答案
相关题目


 在
在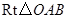 中,
中,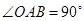 ,且点
,且点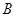 的坐标为(4,2).
的坐标为(4,2).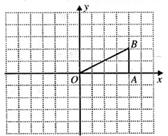
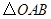 绕点
绕点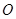 逆时针旋转
逆时针旋转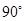 后的
后的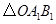 ;
;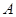 旋转到点
旋转到点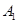 所经过的路线长.
所经过的路线长.
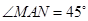 ,
,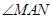 绕点
绕点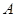 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交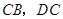 (或它们的延长线)于点
(或它们的延长线)于点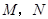 .
.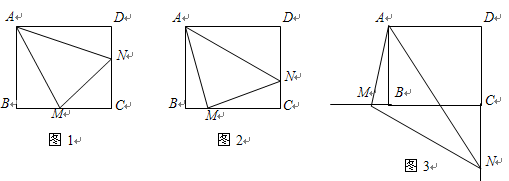
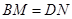 时(如图1),求证:
时(如图1),求证: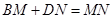 ;
; 时(如图2),则线段
时(如图2),则线段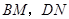 和
和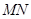 之间数量关系是 ;
之间数量关系是 ;
