题目内容
【题目】已知:抛物线![]() :
:![]() 与抛物线
与抛物线![]() 关于y轴对称, 抛物线
关于y轴对称, 抛物线![]() 与x轴分别交于点A(-3, 0), B(m, 0), 顶点为M.
与x轴分别交于点A(-3, 0), B(m, 0), 顶点为M.
(1)求b和m的值;
(2)求抛物线![]() 的解析式;
的解析式;
(3)在x轴, y轴上分别有点P(t, 0), Q(0, -2t), 其中t>0, 当线段PQ与抛物线![]() 有且只有一个公共点时,求t的取值范围.
有且只有一个公共点时,求t的取值范围.

【答案】(1) m=-1;(2) y=2x2-8x+6;(3) 当1≤t<3或t=![]() 时,PQ与抛物线C2有且仅有一个公共点.
时,PQ与抛物线C2有且仅有一个公共点.
【解析】(1)把A(-3,0)代入y=2x2+bx+6,即可求得b的值,从而求得解析式,令y=0,j解方程即可求得m的值;
(2)根据C1:y=2x2+8x+6=2(x+2)2-2,求得顶点M(-2,-2),即可求得点M关于y轴的对称点N(2,-2),由于a的值不变,根据顶点得出C2:y=2(x-2)2-2=2x2-8x+6;
(3)根据P、Q的坐标求得直线PQ的解析式,然后分三种情况讨论求得.
(1)∵抛物线y=2x2+bx+6过点A(-3,0),
∴0=18-3b+6,
∴b=8,
∴C1:y=2x2+8x+6,
令y=0,则2x2+8x+6=0,
解得x1=-3,x2=-1
∴m=-1;
(2)∵C1:y=2x2+8x+6=2(x+2)2-2,
∴M(-2,-2),
∴点M关于y轴的对称点N(2,-2),
∴C2:y=2(x-2)2-2=2x2-8x+6,
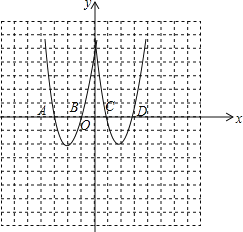
(3)由题意,点A(-3,0)与D,点B(-1,0)与C关于y轴对称,
∴D(3,0),C(1,0),
∵P(t,0),Q(0,-2t),
∴PQ:y=2x-2t,
当PQ过点C时,即P与C重合时,t=1,
当PQ过点D时,即P与D重合时,t=3,
当直线PQ与抛物线C2有且仅有一个公共点时,即方程2x2-8x+6=2x-2t中△=0,
方程整理得x2-5x+3+t=0,△=25-4(3+t)=0,
解得t=![]() .
.
综上,由图得,当1≤t<3或t=![]() 时,PQ与抛物线C2有且仅有一个公共点.
时,PQ与抛物线C2有且仅有一个公共点.

【题目】下表是某校七﹣九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同,但表格中九年级的两个数据被遮盖了,记得九年级文艺小组活动次数与科技小组活动次数相同.
年级 | 课外小组活动总时间(单位:h) | 文艺小组活动次数 | 科技小组活动次数 |
七年级 | 17 | 6 | 8 |
八年级 | 14.5 | 5 | 7 |
九年级 | 12.5 |
|
|
则九年级科技小组活动的次数是_____.