题目内容
【题目】如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.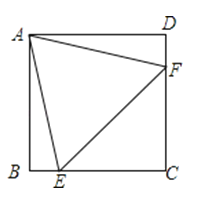
【答案】解:∵在正方形ABCD中,
∴AB=AD,
∵AE=AF,
∴在Rt△ABE和Rt△ADF中
∵ ![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵EC的长为x,
∴FC=x,BE=4﹣x,DF=4﹣x,
∴△AEF的面积为:
y=16﹣S△ABF﹣S△ADE﹣S△EFC
=16﹣![]() ×4(4﹣x)﹣
×4(4﹣x)﹣![]() ×4(4﹣x)﹣
×4(4﹣x)﹣![]() x2
x2
=﹣![]() x2+4x(0<x<4).
x2+4x(0<x<4).
【解析】首先求出Rt△ABF≌Rt△ADE,进而得出△AEF的面积为:y=16﹣S△ABF﹣S△ADE﹣S△EFC即可.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
【题目】某车间一周内计划每天生产100辆电动车,由于工人实行轮休,每天上班人数不一定相等,实际每天生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | ﹣5 | +5 | ﹣5 | +5 | +10 | ﹣10 | ﹣15 |
(1)本周三生产了多少辆电动车?
(2)本周总产量与计划总生产量相比,是增加多少辆?还是减少多少辆?
(3)产量最多的一天比产量最少的一天多生产了多少辆?
(4)请你用折线图画出电动车产量的变化情况.