题目内容
【题目】正比例函数y=x与反比例函数y=
的图象相交于A、C两点．AB⊥x轴于B，CD⊥x轴于D（如图），则四边形ABCD的面积为（ ）
A．1 B．
C．2 D．
【答案】C
【解析】
试题分析：首先根据反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
|k|，得出S△AOB=S△ODC=，再根据反比例函数的对称性可知：OB=OD，得出S△AOB=S△ODA，S△ODC=S△OBC，最后根据四边形ABCD的面积=S△AOB+S△ODA+S△ODC+S△OBC，得出结果．
解：根据反比例函数的对称性可知：OB=OD，AB=CD，
∴四边形ABCD的面积=S△AOB+S△ODA+S△ODC+S△OBC=1×2=2．
故选C．
练习册系列答案
相关题目
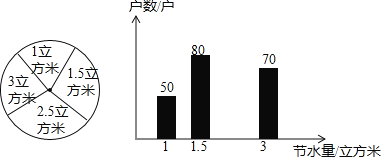
【题目】 “节约用水、人人有责”，某班学生利用课余时间对金辉小区300户居民的用水情况进行了统计，发现5月份各户居民的用水量比4月份有所下降，并且将5月份各户居民的节水量统计整理成如图所示的统计图表
节水量/立方米 | 1 | 1.5 | 2.5 | 3 |
户数/户 | 50 | 80 | a | 70 |
（1）写出统计表中a的值和扇形统计图中2.5立方米对应扇形的圆心角度数．
（2）根据题意，将5月份各居民的节水量的条形统计图补充完整．
（3）求该小区300户居民5月份平均每户节约用水量，若用每立方米水需4元水费，请你估算每户居民1年可节约多少元钱的水费？
