Question

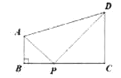
【题目】如图,四边形ABCD中,AB∥CD,∠B=90°,AB=1,CD=2,BC=3,点P为BC边上一动点,若△PAB与△PCD是相似三角形,则BP的长为 _____________

Answer 1

【答案】1或2

【解析】

设BP=x，则CP=BC－BP=3－x，易证∠B=∠C=90°，根据相似三角形的对应顶点分类讨论：①若△PAB∽△PDC时，列出比例式即可求出BP；②若△PAB∽△DPC时，原理同上.

解：设BP=x，则CP=BC－BP=3－x

∵AB∥CD,∠B=90°,

∴∠C=180°－∠B=90°

①若△PAB∽△PDC时

∴

即

解得：x=1

即此时BP=1；

②若△PAB∽△DPC时

∴

即

解得：

即此时BP=1或2；

综上所述：BP=1或2.

故答案为：1或2.