题目内容
【题目】如图,山坡上有一颗树AB,树底部B点到山脚C点的距离BC为6 ![]() 米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)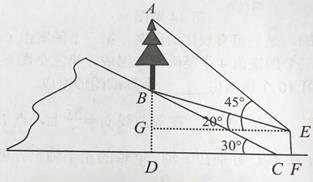
【答案】解:在Rt△BCD中,CD=BC×cos∠BCD=6![]() ×
×![]() =9,
=9,
则DF=CD+CF=10(米),
∵四边形GDFE为矩形,
∴GE=DF=10(米),
∵∠AEG=45°,
∴AG=GE=10(米),
在Rt△BEG中,BG=GE×tan∠BEG≈10×0.36=3.6(米),
则AB=AG-BG=10-3.6=6.4(米).
答:旗杆AB的高度为6.4米.
【解析】根据AB=AG-BG,先求出AG和BG,在Rt△ABG中,∠AEG=45°,则AG=GE=DF=CD+CF,需要求出CD,BC已知,∠BCD的度数已知,可求得;在在Rt△BEG中,∠BEG已知,GE前面已求得,则解答案完成.

练习册系列答案
相关题目