题目内容
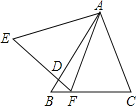
【题目】在△ABC中,F是BC上一点,FG⊥AB,垂足为G.
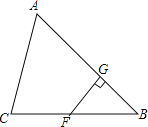
(1)过C点画CD⊥AB,垂足为D;
(2)过D点画DE∥BC,交AC于E;
(3)求证:∠EDC=∠GFB.
【答案】见解析
【解析】
试题分析:(1)以C为圆心画弧,与AB交于两点,分别以两点为圆心,大于两点距离一半长为半径画弧,两弧交于一点,作出垂直CD即可;
(2)以D为顶点,作∠ADE=∠B,利用同位角相等两直线平行即可确定出DE;
(3)由FG与CD都与AB垂直,得到FG与CD平行,利用两直线平行同位角相等得到一对角相等,再由DE与BC平行,得到一对内错角相等,等量代换即可得证.
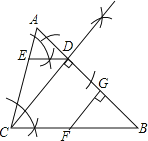
解:(1)画CD⊥AB,如图所示;
(2)画DE∥BC,如图所示;
(3)证明:∵FG⊥AB,CD⊥AB,
∴∠FGB=∠CDB=90°,
∴FG∥CD,
∴∠DFB=∠DCB,
∵DE∥BC,
∴∠EDC=∠DCB,
∴∠EDC=∠GFB.

练习册系列答案
相关题目