题目内容
【题目】已知:如图①,在平行四边形ABCD中,AB=12,BC=6,AD⊥BD.以AD为斜边在平行四边形ABCD的内部作Rt△AED,∠EAD=30°,∠AED=90°.
(1)求△AED的周长;
(2)若△AED以每秒2个单位长度的速度沿DC向右平行移动,得到△A0E0D0,当A0D0与BC重合时停止移动,设运动时间为t秒,△A0E0D0与△BDC重叠的面积为S,请直接写出S与t之间的函数关系式,并写出t的取值范围;
(3)如图②,在(2)中,当△AED停止移动后得到△BEC,将△BEC绕点C按顺时针方向旋转α(0°<α<180°),在旋转过程中,B的对应点为B1,E的对应点为E1,设直线B1E1与直线BE交于点P、与直线CB交于点Q.是否存在这样的α,使△BPQ为等腰三角形?若存在,求出α的度数;若不存在,请说明理由.

【答案】(1)![]() (2)
(2)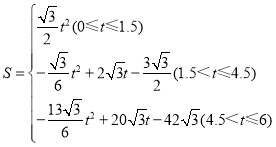 (3)存在α=30°,75°或165°,使△BPQ为等腰三角形
(3)存在α=30°,75°或165°,使△BPQ为等腰三角形
【解析】
试题分析:(1)在Rt△ADE中,解直角三角形即可;
(2)在△AED向右平移的过程中:
(I)当0≤t≤1.5时,如答图1所示,此时重叠部分为一个三角形;
(II)当1.5<t≤4.5时,如答图2所示,此时重叠部分为一个四边形;
(III)当4.5<t≤6时,如答图3所示,此时重叠部分为一个五边形.
(3)根据旋转和等腰三角形的性质进行探究,结论是:存在α(30°和75°),使△BPQ为等腰三角形.如答图4、答图5所示.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AD=BC=6.
在Rt△ADE中,AD=6,∠EAD=30°,
∴AE=ADcos30°=3![]() ,DE=ADsin30°=3,
,DE=ADsin30°=3,
∴△AED的周长为:6+3+3![]() =9+3
=9+3![]() .
.
(2)在△AED向右平移的过程中:
(I)当0≤t≤1.5时,如答图1所示,此时重叠部分为△D0NK.
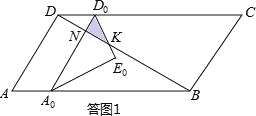
∵DD0=2t,∴ND0=DD0sin30°=t,NK=ND0÷tan30°=![]() t,
t,
∴S=S△D0NK=![]() ND0NK=
ND0NK=![]() t
t![]() t=
t=![]() t2;
t2;
(II)当1.5<t≤4.5时,如答图2所示,此时重叠部分为四边形D0E0KN.
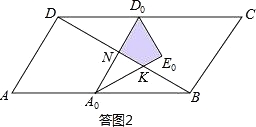
∵AA0=2t,∴A0B=AB﹣AA0=12﹣2t,
∴A0N=![]() A0B=6﹣t,NK=A0Ntan30°=
A0B=6﹣t,NK=A0Ntan30°=![]() (6﹣t).
(6﹣t).
∴S=![]() =
=![]() ×3×3
×3×3![]() ﹣
﹣![]() ×(6﹣t)×
×(6﹣t)×![]() (6﹣t)=
(6﹣t)=![]() t2+
t2+![]() t﹣
t﹣![]() ;
;
(III)当4.5<t≤6时,如答图3所示,此时重叠部分为五边形D0IJKN.
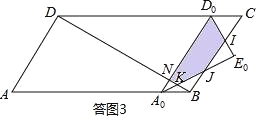
∵AA0=2t,∴A0B=AB﹣AA0=12﹣2t=D0C,
∴A0N=![]() A0B=6﹣t,D0N=6﹣(6﹣t)=t,BN=A0Bcos30°=
A0B=6﹣t,D0N=6﹣(6﹣t)=t,BN=A0Bcos30°=![]() (6﹣t);
(6﹣t);
易知CI=BJ=A0B=D0C=12﹣2t,∴BI=BC﹣CI=2t﹣6,
S=S梯形BND0I﹣S△BKJ=![]() [t+(2t﹣6)]·
[t+(2t﹣6)]·![]() (6﹣t)﹣
(6﹣t)﹣![]() ·(12﹣2t)
·(12﹣2t)![]() (12﹣2t)=
(12﹣2t)=![]() t2+
t2+![]() t﹣
t﹣![]() .
.
综上所述,S与t之间的函数关系式为:
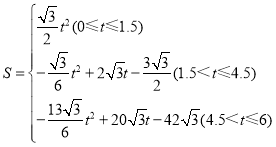 .
.
(3)存在α,使△BPQ为等腰三角形.
理由如下:经探究,得△BPQ∽△B1QC,
故当△BPQ为等腰三角形时,△B1QC也为等腰三角形.
(I)当QB=QP时(如答图4),
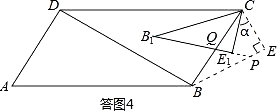
则QB1=QC,∴∠B1CQ=∠B1=30°,
即∠BCB1=30°,
∴α=30°;
(II)当BQ=BP时,则B1Q=B1C,
若点Q在线段B1E1的延长线上时(如答图5),
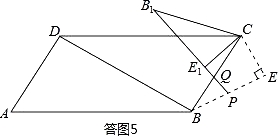
∵∠B1=30°,∴∠B1CQ=∠B1QC=75°,
即∠BCB1=75°,
∴α=75°;
若点Q在线段E1B1的延长线上时(如答图6),
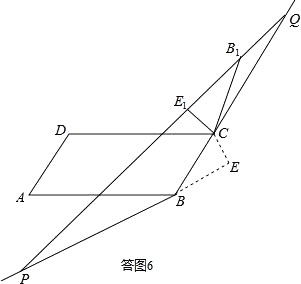
∵∠CB1E1=30°,∴∠B1CQ=∠B1QC=15°,
即∠BCB1=180°﹣∠B1CQ=180°﹣15°=165°,
∴α=165°.
③当PQ=PB时(如答图7),则CQ=CB1,
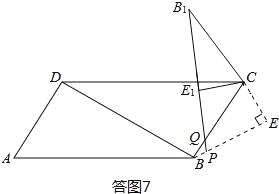
∵CB=CB1,
∴CQ=CB1=CB,
又∵点Q在直线CB上,0°<α<180°,
∴点Q与点B重合,
此时B、P、Q三点不能构成三角形.
综上所述,存在α=30,75°或165°,使△BPQ为等腰三角形.

 名校课堂系列答案
名校课堂系列答案
