题目内容
已知抛物线y=-
x2+bx+c的顶点为P,与x轴的正半轴交于A(x1,0)、B(x2,0)(x1<x2)两点,与y轴交于点C,PA是△ABC的外接圆的切线.设M(0,-
),若AM∥BC,求抛物线的解析式.
| 1 |
| 6 |
| 3 |
| 2 |
分析:利用公式法求出抛物线的顶点坐标,再令x=0,求出此时对应的y值,即C的纵坐标,设△ABC的外接圆的圆心为D,则点P和点D都在线段AB的垂直平分线上,设点D的坐标为(3b,m).再利用根与系数的关系求出AE的值,利用射影定理和切线的性质即可求出m的值,进而求出c的值,最后利用相似三角形的性质求出b的值,从而求出抛物线的解析式.
解答: 解:∵抛物线y=-
解:∵抛物线y=-
x2+bx+c中,
a′=-
,b′=b,c′=c,
∴点P的横坐标为:-
=3b,纵坐标为:
=
b2+c,
∴点P的坐标为(3b,
b2+c),
令x=0,则y=c,
∴点C(0,c),
设△ABC的外接圆的圆心为D,则点P和点D都在线段AB的垂直平分线上,设点D的坐标为(3b,m).
显然,x1,x2是一元二次方程-
x2+bx+c=0的两根,
∴x1=3b-
,x2=3b+
,
又∵AB的中点E的坐标为(3b,0),
∴AE=
.
∵PA为⊙D的切线,
∴PA⊥AD,
又∵AE⊥PD,
∴由射影定理可得 AE2=PE•DE,即(
)2=(
b2+c)•|m|,又易知m<0,
∴可得m=-6,
又∵DA=DC得 DA2=DC2,即(
)2+m2=(3b-0)2+(m-c)2,
把m=-6代入后可解得c=-6(另一解c=0舍去).
又∵AM∥BC,
∴
=
,即
=
.…
把c=-6代入,解得b=
,(另一解b=-
舍去).
∴抛物线的解析式为y=-
x2+
x-6.
 解:∵抛物线y=-
解:∵抛物线y=-| 1 |
| 6 |
a′=-
| 1 |
| 6 |
∴点P的横坐标为:-
| b′ |
| 2a′ |
| 4a′c′-b′ 2 |
| 4a′ |
| 3 |
| 2 |
∴点P的坐标为(3b,
| 3 |
| 2 |
令x=0,则y=c,
∴点C(0,c),
设△ABC的外接圆的圆心为D,则点P和点D都在线段AB的垂直平分线上,设点D的坐标为(3b,m).
显然,x1,x2是一元二次方程-
| 1 |
| 6 |
∴x1=3b-
| 9b2+6c |
| 9b2+6c |
又∵AB的中点E的坐标为(3b,0),
∴AE=
| 9b2+6c |
∵PA为⊙D的切线,
∴PA⊥AD,
又∵AE⊥PD,
∴由射影定理可得 AE2=PE•DE,即(
| 9b2+6c |
| 3 |
| 2 |
∴可得m=-6,
又∵DA=DC得 DA2=DC2,即(
| 9b2+6c |
把m=-6代入后可解得c=-6(另一解c=0舍去).
又∵AM∥BC,
∴
| OA |
| OB |
| OM |
| OC |
3b-
| ||
3b+
|
|-
| ||
| |-6| |
把c=-6代入,解得b=
| 5 |
| 2 |
| 5 |
| 2 |
∴抛物线的解析式为y=-
| 1 |
| 6 |
| 5 |
| 2 |
点评:本题综合性的考查了二次函数的各种性质、圆的切线的性质、平行线的性质、射影定理的运用,根与系数的关系以及相似三角形的判定和性质,题目的难度非常大.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
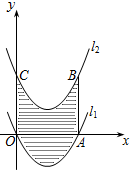 如图,已知抛物线l1:y=
如图,已知抛物线l1:y=| 1 |
| 2 |
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
 半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.