题目内容
【题目】如图,四边形ABCD为平行四边形,∠BAD的平分线AE交CD于点F,交BC的延长线于点E.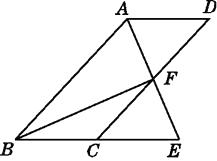
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求ABCD的面积.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠DAE=∠E.
又∵AE平分∠BAD,∴∠BAE=∠DAE.∴∠BAE=∠E.
∴BA=BE=CD.
(2)解:∵∠BEA=60°,BA=BE,
∴△ABE为等边三角形.
∵BF⊥AE,
∴F为AE的中点.
∴AF=EF
在△AFD和△EFC中,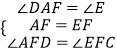
∴△AFD≌△EFC(ASA).
∴△AFD的面积等于△EFC的面积.
∴ABCD的面积等于△ABE的面积.
在△ABE中,AB=AE=4,
∴AF=2.由勾股定理得BF=2 ![]() ,
,
∴△ABE的面积= ![]() ×4×2
×4×2 ![]() =4
=4 ![]() .
.
∴ABCD的面积为4 ![]()
【解析】(1)根据平行四边形的性质证明AD∥BC,BA=CD,再根据键盘侠的定义及平行线的性质证明∠BAE=∠E,根据等角对等边得出AB=BE,从而可证得结论。
(2)根据已知条件∠BEA=60°,BA=BE,可证得△ABE为等边三角形,再根据等边三角形三线合一的性质证明AF=EF,就可证明△AFD≌△EFC,根据全等三角形的面积相等,要求ABCD的面积就转化为求△ABE得面积,然后在△ABE中,利用勾股定理求出BF的长,利用三角形的面积公式就可求出答案。

练习册系列答案
相关题目