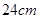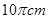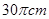题目内容
如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
小题1:求证:直线CD为⊙O的切线;
小题2:当AB=2BE,且CE=时,求AD的长.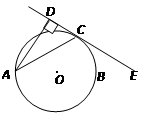
小题1:求证:直线CD为⊙O的切线;
小题2:当AB=2BE,且CE=时,求AD的长.

小题1:略
小题2:


解:(1)连接OC,
∵AC平分∠DAB,
∴∠1=∠2,
∵又AO=CO,
∴∠3=∠2,
∴∠1=∠3,
∴OC∥AD,
∵又CD⊥AD,
∴CD⊥OC,
∴CD为⊙O的切线;
(2)∵直径AB=2BE,
∴OE=2OC,
在Rt△EOC中,设CO=x,即OE=2x,
由勾股定理得:CE=
 x,
x,又∵CE=
 ,
,∴x=1
即OC=1,
∵OC∥AD(已证)
∴△EOC∽△EAD,
∴
 ,
,即
 ,
, ∴AD=
 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
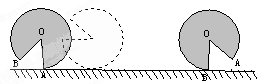
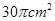 的扇形
的扇形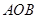 ,半径
,半径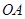 与地面垂直,在没有滑动的情况下,将扇形向右滚动至
与地面垂直,在没有滑动的情况下,将扇形向右滚动至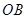 与地面垂直为止,则O点移动的距离为( )
与地面垂直为止,则O点移动的距离为( )