题目内容
已知关于x的方程kx2-(4k+1)x+4=0.
(1)当k取何值时,方程有两个实数根;
(2)若二次函数y=kx2-(4k+1)x+4的图象与x轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标;
(3)若(2)中的抛物线与x轴交于A、B两点,与y轴交于C点.将抛物线向上平移n个单位,使平移后得到的抛物线的顶点落在△ABC的内部(不包括△ABC的边界),写出n的取值范围.
解:(1)△=b2-4ac=[-(4k+1)]2-4×4k≥0,
整理得,(4k-1)2≥0,
∴对于k≠0的任何实数,关于x的方程kx2-(4k+1)x+4=0总有两个实数根;
(2)令y=0,则kx2-(4k+1)x+4=0,
即(kx-1)(x-4)=0,
解得x1= ,x2=4,
,x2=4,
∵函数图象与x轴两个交点的横坐标均为整数,k为正整数,
∴k=1,
∴二次函数解析式为y=x2-5x+4,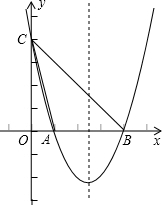
∵y=x2-5x+4,
=x2-5x+ -
- +4,
+4,
=(x- )2-
)2- ,
,
∴抛物线的顶点坐标为( ,-
,- );
);
(3)由(2)得,点A(1,0),B(4,0),
令x=0,则y=4,
∴点C的坐标为(0,4),
设直线BC的解析式为y=kx+b(k≠0),
则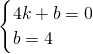 ,
,
解得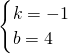 ,
,
∴直线BC的解析式为y=-x+4,
∵二次函数的对称轴为直线x= ,
,
∴当x= 时,y=-
时,y=- +4=
+4= ,
,
∵ -(-
-(- )=
)= +
+ =
= ,
,
∴当抛物线的顶点落在△ABC的内部时, <n<
<n< .
.
分析:(1)利用根的判别式△≥0列式计算即可得解;
(2)令y=0,利用因式分解法解一元二次方程求解,再根据两交点的横坐标均为整数,k为正整数确定出k的值,从而得到二次函数的解析式,然后配方成顶点式解析式,再写出顶点坐标即可;
(3)根据二次函数解析式求出点A、B、C的坐标,再利用待定系数法求出直线BC的解析式,然后求出与对称轴的交点坐标,再根据平移的性质确定出n的取值范围即可.
点评:本题是二次函数综合题型,主要利用了根的判别式,待定系数法求二次函数解析式,待定系数法求一次函数解析式以及配方法,(1)要注意二次项的系数不等于0,(2)根据与x轴的交点的横坐标是整数判断出k的值是解题的关键,(3)求出直线BC与对称轴的交点是解题的关键,作出图形更形象直观.
整理得,(4k-1)2≥0,
∴对于k≠0的任何实数,关于x的方程kx2-(4k+1)x+4=0总有两个实数根;
(2)令y=0,则kx2-(4k+1)x+4=0,
即(kx-1)(x-4)=0,
解得x1=
 ,x2=4,
,x2=4,∵函数图象与x轴两个交点的横坐标均为整数,k为正整数,
∴k=1,
∴二次函数解析式为y=x2-5x+4,

∵y=x2-5x+4,
=x2-5x+
 -
- +4,
+4,=(x-
 )2-
)2- ,
,∴抛物线的顶点坐标为(
 ,-
,- );
);(3)由(2)得,点A(1,0),B(4,0),
令x=0,则y=4,
∴点C的坐标为(0,4),
设直线BC的解析式为y=kx+b(k≠0),
则
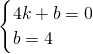 ,
,解得
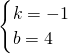 ,
,∴直线BC的解析式为y=-x+4,
∵二次函数的对称轴为直线x=
 ,
,∴当x=
 时,y=-
时,y=- +4=
+4= ,
,∵
 -(-
-(- )=
)= +
+ =
= ,
,∴当抛物线的顶点落在△ABC的内部时,
 <n<
<n< .
.分析:(1)利用根的判别式△≥0列式计算即可得解;
(2)令y=0,利用因式分解法解一元二次方程求解,再根据两交点的横坐标均为整数,k为正整数确定出k的值,从而得到二次函数的解析式,然后配方成顶点式解析式,再写出顶点坐标即可;
(3)根据二次函数解析式求出点A、B、C的坐标,再利用待定系数法求出直线BC的解析式,然后求出与对称轴的交点坐标,再根据平移的性质确定出n的取值范围即可.
点评:本题是二次函数综合题型,主要利用了根的判别式,待定系数法求二次函数解析式,待定系数法求一次函数解析式以及配方法,(1)要注意二次项的系数不等于0,(2)根据与x轴的交点的横坐标是整数判断出k的值是解题的关键,(3)求出直线BC与对称轴的交点是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
 -kx-6=0的一个根为3,则实数k的值为(
)
-kx-6=0的一个根为3,则实数k的值为(
)