题目内容
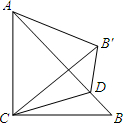 (2013•黄州区二模)等腰直角△ABC中,∠ACB=90°,D为AB上一点,沿CD翻折,B落在△ABC所在平面中的B′处,∠BAB′=25°,则∠ADC=
(2013•黄州区二模)等腰直角△ABC中,∠ACB=90°,D为AB上一点,沿CD翻折,B落在△ABC所在平面中的B′处,∠BAB′=25°,则∠ADC=70°
70°
.分析:根据折叠可得:∠1=∠2,BC=CB′,然后根据等腰直角三角形的性质得到AC=BC,∠CAB=∠B=45°,再计算出∠CAB′的度数,进而可算出∠ACE的度数,再根据∠ACB=90°,可算出∠1+∠2的和,再根据三角形的外角和内角的关系计算出∠CDA的度数.
解答: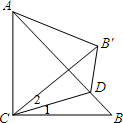 解:根据折叠可得:∠1=∠2,BC=CB′,
解:根据折叠可得:∠1=∠2,BC=CB′,
∵△ABC是等腰直角三角形,
∴AC=BC,∠CAB=∠B=45°,
∴AC=CB′,
∴∠AB′C=∠CAB′,
∵∠BAB′=25°,
∴∠CAB′=45°+25°=70°,
∴∠AB′C=70°,
∴∠ACB′=180°-70°-70°=40°,
∵∠ACB=90°,
∴∠B′CB=50°,
∵∠1=∠2,
∴∠1=25°,
∴∠CDA=45°+25°=70°,
故答案为:70°.
 解:根据折叠可得:∠1=∠2,BC=CB′,
解:根据折叠可得:∠1=∠2,BC=CB′,∵△ABC是等腰直角三角形,
∴AC=BC,∠CAB=∠B=45°,
∴AC=CB′,
∴∠AB′C=∠CAB′,
∵∠BAB′=25°,
∴∠CAB′=45°+25°=70°,
∴∠AB′C=70°,
∴∠ACB′=180°-70°-70°=40°,
∵∠ACB=90°,
∴∠B′CB=50°,
∵∠1=∠2,
∴∠1=25°,
∴∠CDA=45°+25°=70°,
故答案为:70°.
点评:此题主要考查了图形的翻折变换,以及三角形内角和定理,三角形内角与外角的性质,关键是找准翻折后相等的对应边和对应角.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
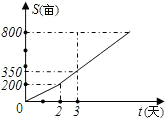 (2013•黄州区二模)某农场租用收割机收割小麦,甲收割机单独收割2天后,又调来乙收割机参与收割,直至完成800亩的收割任务.收割亩数与天数之间的函数关系如图所示,那么乙参与收割的天数是
(2013•黄州区二模)某农场租用收割机收割小麦,甲收割机单独收割2天后,又调来乙收割机参与收割,直至完成800亩的收割任务.收割亩数与天数之间的函数关系如图所示,那么乙参与收割的天数是