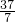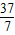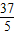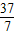题目内容
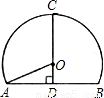
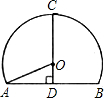 如图,是一个圆曲隧道的截面,若路面AB宽为10米,净高CD为7米,则此隧道圆的半径OA是( )
如图,是一个圆曲隧道的截面,若路面AB宽为10米,净高CD为7米,则此隧道圆的半径OA是( )| A、5 | ||
B、
| ||
C、
| ||
| D、7 |
分析:根据垂径定理得到AD=DB=
AB=
×10=5m,设半径OA=R,OD=CD-R=7-R,在Rt△OAD中根据勾股定理得R2=(7-R)2+52,然后解方程求出R即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵OD⊥AB,
∴AD=DB=
AB=
×10=5m,
在Rt△OAD中,设半径OA=R,OD=CD-R=7-R,
∴OA2=OD2+AD2,即R2=(7-R)2+52,解得R=
,
∴此隧道圆的半径OA是
m.
故选B.
∴AD=DB=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OAD中,设半径OA=R,OD=CD-R=7-R,
∴OA2=OD2+AD2,即R2=(7-R)2+52,解得R=
| 37 |
| 7 |
∴此隧道圆的半径OA是
| 37 |
| 7 |
故选B.
点评:本题考查了垂径定理的应用:先从实物图中得到几何图形----圆,然后利用垂径定理(垂直于弦的直径平分弦,并且平分弦所对的弧)得到等线段,最后利用勾股定理建立等量关系,解方程求解.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 如图,是一个圆曲隧道的截面,若路面AB宽为10米,净高CD为7米,则此隧道圆的半径OA是
如图,是一个圆曲隧道的截面,若路面AB宽为10米,净高CD为7米,则此隧道圆的半径OA是