题目内容
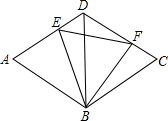 (2012•海门市模拟)如图,菱形ABCD的边长为1,BD=1,E,F分别是边AD,CD上的两个动点,且满足AE+CF=1,设△BEF的面积为s,则s的取值范围是( )
(2012•海门市模拟)如图,菱形ABCD的边长为1,BD=1,E,F分别是边AD,CD上的两个动点,且满足AE+CF=1,设△BEF的面积为s,则s的取值范围是( )分析:利用菱形的性质和正三角形的特点可证得△BDE≌△BCF;继而可得△BEF为正三角形,然后作出恰当的辅助线,构成直角三角形,根据直角三角形的特点和三角函数进行计算即可求得答案.
解答: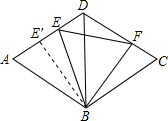 解:菱形ABCD的边长为1,BD=1,
解:菱形ABCD的边长为1,BD=1,
∴△ABD和△BCD都为正三角形,
∴∠BDE=∠BCF=60°,BD=BC,
∵AE+DE=AD=1,而AE+CF=1,
∴DE=CF,
在△BDE和△BCF中,
,
∴△BDE≌△BCF(SAS);
∴∠DBE=∠CBF,BE=BF,
∵∠DBC=∠DBF+∠CBF=60°,
∴∠DBF+∠DBE=60°即∠EBF=60°,
∴△BEF为正三角形;
设BE=BF=EF=x,
则S=
•x•x•sin60°=
x2,
当BE⊥AD时,x最小为:1×sin60°=
,
∴S最小=
×(
)2=
,
当BE与AB重合时,x最大,
∵菱形ABCD的边长为1,
∴AB=1,
∴x最大为1,
∴S最大=
×12=
,
∴
≤s≤
.
故选C.
 解:菱形ABCD的边长为1,BD=1,
解:菱形ABCD的边长为1,BD=1,∴△ABD和△BCD都为正三角形,
∴∠BDE=∠BCF=60°,BD=BC,
∵AE+DE=AD=1,而AE+CF=1,
∴DE=CF,
在△BDE和△BCF中,
|
∴△BDE≌△BCF(SAS);
∴∠DBE=∠CBF,BE=BF,
∵∠DBC=∠DBF+∠CBF=60°,
∴∠DBF+∠DBE=60°即∠EBF=60°,
∴△BEF为正三角形;
设BE=BF=EF=x,
则S=
| 1 |
| 2 |
| ||
| 4 |
当BE⊥AD时,x最小为:1×sin60°=
| ||
| 2 |
∴S最小=
| ||
| 4 |
| ||
| 2 |
3
| ||
| 16 |
当BE与AB重合时,x最大,
∵菱形ABCD的边长为1,
∴AB=1,
∴x最大为1,
∴S最大=
| ||
| 4 |
| ||
| 4 |
∴
3
| ||
| 16 |
| ||
| 4 |
故选C.
点评:此题考查了菱形的性质、等边三角形的判定与性质以及三角形的面积问题.此题难度较大,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
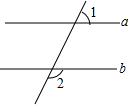 (2012•海门市模拟)如图,直线a∥b,若∠1=40°,则∠2=
(2012•海门市模拟)如图,直线a∥b,若∠1=40°,则∠2= (2012•海门市模拟)一副直角三角板如图放置,点A在DF的延长线上,BC∥DA,∠D=∠BAC=90°,∠C=45°,∠E=30°,AC=10.
(2012•海门市模拟)一副直角三角板如图放置,点A在DF的延长线上,BC∥DA,∠D=∠BAC=90°,∠C=45°,∠E=30°,AC=10.