题目内容
【题目】如图，在正方形ABCD中，点E是AB上一动点（不与点A，B重合），点F在AD上，过点E作EG⊥EF交BC于点G，连接FG．
（1）当BE=AF时，求证：EF=EG
（2）若AB=4，AF=1，且设AE=n，
①当FG∥AB时，求n的值；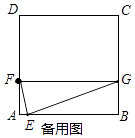
【答案】
（1）
∵四边形ABCD是正方形，
∴∠A=∠B=90°，
∵EG⊥EF，
∴∠AEF+∠BEG=90°，
∵∠AFE+∠AEF=90°，
∴∠AFE=∠BEG，
在△AEF和△BGE中，
，
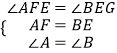∴△AEF≌△BGE（ASA），
∴EF=EG；
（2）
∵FG∥AB，
∴BG=AF=1，
∵AB=4，AE=n，
∴BE=4﹣n，
由（1）可得∠A=∠B=90°，∠AFE=∠BEG，
∴△AEF∽△BGE，
∴ 
= 
，即 
= 
，
∴解得n1=2﹣ 
，n2=2+ ；
②当BG取最大值时，求△EFG的面积．
∵△AEF∽△BGE，
∴ = ，
∴BG= 
=n（4﹣n）=﹣n2+4n=﹣（n﹣2）2+4，
∴当n=2时，BG有最大值4，
此时点G与点C重合，
∴EF= 
= 
= 
，
EG= 
= 
=2 ，
∴△EFG的面积= 
EG×EF= × ×2 =5．
【解析】（1）根据正方形的性质，判定△AEF≌△BGE，即可得出EF=EG；（2）①根据∠A=∠B=90°，∠AFE=∠BEG，即可判定△AEF∽△BGE，进而得到 = ，即 
= ，据此可得n的值；②根据△AEF∽△BGE，得出 = ，即BG= =n（4﹣n）=﹣n2+4n=﹣（n﹣2）2+4，进而得到当n=2时，BG有最大值4，据此可得点G与点C重合，再根据勾股定理求得EF= = ，EG= =2 ，最后根据△EFG的面积= EG×EF进行计算即可．
【考点精析】本题主要考查了全等三角形的性质和相似三角形的性质的相关知识点，需要掌握全等三角形的对应边相等; 全等三角形的对应角相等；对应角相等，对应边成比例的两个三角形叫做相似三角形才能正确解答此题．
