��Ŀ����
����Ŀ���龳�۲죺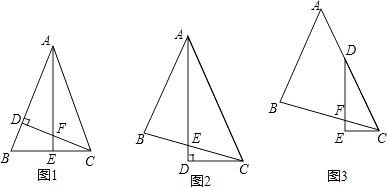
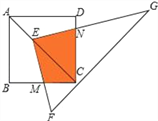
��1����ͼ1����ABC�У�AB=AC����BAC=45�㣬CD��AB��AE��BC������ֱ�ΪD��E��CD��AE���ڵ�F��
��д��ͼ1�����е�ȫ����������
���߶�AF���߶�CE��������ϵ�� ��
��2������̽����
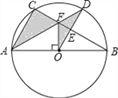
��ͼ2����ABC�У���BAC=45�㣬AB=BC��ADƽ�֡�BAC��AD��CD������ΪD��AD��BC���ڵ�E��
��֤��AE=2CD��
��3����չ���죺
��ͼ3����ABC�У���BAC=45�㣬AB=BC����D��AC�ϣ���EDC= ![]() ��BAC��DE��CE������ΪE��DE��BC���ڵ�F����֤��DF=2CE��
��BAC��DE��CE������ΪE��DE��BC���ڵ�F����֤��DF=2CE��
Ҫ������д�������ߵ�����������ͼ3�л��������ߣ�����Ҫ֤����
���𰸡�
��1����ABE�ա�ACE����ADF�ա�CDB��AF=2CE
��2���⣺֤�����ӳ�AB��CD���ڵ�G����ͼ2��ʾ��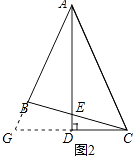
��ADƽ�֡�BAC��
���CAD=��GAD��
��AD��CD��
���ADC=��ADG=90�㣬
�ڡ�ADC�͡�ADG�У� ��
��
���ADC�ա�ADG��ASA����
��CD=GD����CG=2CD��
�ߡ�BAC=45�㣬AB=BC��
���ABC=90�㣬
���CBG=90�㣬
���G+��BCG=90�㣬
�ߡ�G+��BAE=90�㣬
���BAE=��BCG��
�ڡ�ABE�͡�CBG�У�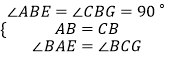 ��
��
���ABE�ա�CBG��ASA����
��AE=CG=2CD
��3���⣺��DG��BC��CE���ӳ�����G��
��ͼ3��ʾ��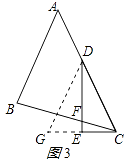
���������⣺��ͼ1�����е�ȫ��������Ϊ��ABE�ա�ACE����ADF�ա�CDB��
�ʴ�Ϊ����ABE�ա�ACE����ADF�ա�CDB
���߶�AF���߶�CE��������ϵ�ǣ�AF=2CE��
�ʴ�Ϊ��AF=2CE��
��1���ٸ��ݵ��������ε����ߺ�һ�ó�BE=CE,Ȼ������SSS�жϳ���ABE�ա�ACE����Rt��ADC�С�DAC=45�㣬�Ӷ��ó�AD=DC ,���ݵȽǵ������ȵó���DAF=��DCB ,�Ӷ�����ASA�жϳ���ADF�ա�CDB ������ȫ�������ζ�Ӧ����ȵó�AF=BC����CE=BE,�Ӷ��ó�AF=2CE ��
��2���ӳ�AB��CD���ڵ�G�����ݽ�ƽ���ߵĶ���ó���CAD=��GAD�����ݴ�ֱ�Ķ���ó���ADC=��ADG=90�㣬�Ӷ�����ASA�жϳ���ADC�ա�ADG ������ȫ�������ε����ʵó�CD=GD����CG=2CD �����ݵ��������ε����ʼ������ε��ڽǺ͵ó���ABC=90�� ����CBG=90�㣬����ͬ�ǵ������ȵó���BAE=��BCG���Ӷ�����ASA�жϳ���ABE�ա�CBG ���Ӷ��ó�AE=CG=2CD ��
��3����DG��BC��CE���ӳ�����G��ͬ��2��֤��������ȫ�ȣ��ó�DF=2CE ��