题目内容
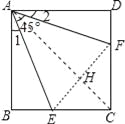
【题目】如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
①∠1=∠2=22.5°; ②点C到EF的距离是![]() -1; ③△ECF的周长为2; ④BE+DF>EF.
-1; ③△ECF的周长为2; ④BE+DF>EF.
其中正确的结论是 .(写出所有正确结论的序号)

【答案】①②③
【解析】试题分析:∵四边形ABCD为正方形, ∴AB=AD,∠BAD=∠B=∠D=90°,
在Rt△ABE和Rt△ADF中![]() , ∴Rt△ABE≌Rt△ADF, ∴∠1=∠2, ∵∠EAF=45°,
, ∴Rt△ABE≌Rt△ADF, ∴∠1=∠2, ∵∠EAF=45°,
∴∠1=∠2=∠22.5°,所以①正确;
连结EF、AC,它们相交于点H,如图,∵Rt△ABE≌Rt△ADF, ∴BE=DF, 而BC=DC, ∴CE=CF,
而AE=AF, ∴AC垂直平分EF,AH平分∠EAF, ∴EB=EH,FD=FH, ∴BE+DF=EH+HF=EF,所以④错误;
∴△ECF的周长=CE+CF+EF=CED+BE+CF+DF=CB+CD=1+1=2,所以③正确;
设BE=x,则EF=2x,CE=1﹣x, ∵△CEF为等腰直角三角形,
∴EF=![]() CE,即2x=
CE,即2x=![]() (1﹣x),解得x=
(1﹣x),解得x=![]() ﹣1, ∴EF=2(
﹣1, ∴EF=2(![]() ﹣1),
﹣1),
∴CH=![]() EF=
EF=![]() ﹣1,所以②正确.
﹣1,所以②正确.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某超市经销一种绿茶,每千克成本为60元,经过市场调查发现,在一段时间内,该种绿茶的销售量y(千克)与销售单价x(元)满足一次函数关系,其变化如下表所示:
销售单价(x元) | 65 | 70 | 75 | 80 |
销售量(y千克) | 110 | 100 | 90 | 80 |
(1)求y与x的函数解析式;
(2)当销售单价为多少元时,该种绿茶的销售利润最大?
(3)如果物价部门规定这种绿茶每千克销售单价不高于95元,若超市计划在这段时间内获得该种绿茶的销售利润为1 600元,其销售单价应定为多少?

