题目内容
已知:如图,在平行四边形ABCD中,DE⊥AB于点E,DF⊥BC于点F,∠DAB的平分线交DE于 点M,交DF于点N,交DC于点P.
点M,交DF于点N,交DC于点P.
(1)求证:∠ADE=∠CDF;
(2)如果∠B=120°,求证:△DMN是等边三角形.
证明:(1)∵四边形ABCD是平行四边形,
∴∠DAB=∠C,DC∥AB,
∵DE⊥AB于点E,DF⊥BC于点F,
∴∠ADE=90°-∠DAB,∠CDF=90°-∠C,
∴∠ADE=∠CDF.
(2)证明:∵∠DAB的平分线交DE于点M,交DF于点N,交DC于点P,
∴∠DAP=∠BAP,
∵DC∥AB,
∴∠DPA=∠BAP,
∴∠DAP=∠DPA,
∴DA=DP,
∵∠ADE=∠CDF,∠DAP=∠DPA,DA=DP,
∴△DAM≌△DPN,
∴DM=DN,
∵∠B=120°,
∴∠MDN=360°-∠DEB-∠EFB-∠B=360°-90°-90°-120°=60°,
∴△DMN是等边三角形.
分析:(1)根据平行四边形的性质得到∠DAB=∠C,DC∥AB,根据三角形的内角和定理和垂线即可求出答案;
(2)根据平行四边形的性质得出DC∥AB,根据角平分线得出∠DAP=∠BAP,推出DA=DP,根据全等三角形的判定证△DAM≌△DPN,推出DN=DM,求出∠MDN60度,即可得到答案.
点评:本题主要考查对平行四边形的性质,三角形的内角和定理,垂线,全等三角形的性质和判定,等边三角形的判定,平行线的性质,角平分线的性质,多边形的内角和定理等知识点的理解和掌握,能综合运用这些性质进行推理是解此题的关键.
∴∠DAB=∠C,DC∥AB,
∵DE⊥AB于点E,DF⊥BC于点F,
∴∠ADE=90°-∠DAB,∠CDF=90°-∠C,
∴∠ADE=∠CDF.
(2)证明:∵∠DAB的平分线交DE于点M,交DF于点N,交DC于点P,
∴∠DAP=∠BAP,
∵DC∥AB,
∴∠DPA=∠BAP,
∴∠DAP=∠DPA,
∴DA=DP,
∵∠ADE=∠CDF,∠DAP=∠DPA,DA=DP,
∴△DAM≌△DPN,
∴DM=DN,
∵∠B=120°,
∴∠MDN=360°-∠DEB-∠EFB-∠B=360°-90°-90°-120°=60°,
∴△DMN是等边三角形.
分析:(1)根据平行四边形的性质得到∠DAB=∠C,DC∥AB,根据三角形的内角和定理和垂线即可求出答案;
(2)根据平行四边形的性质得出DC∥AB,根据角平分线得出∠DAP=∠BAP,推出DA=DP,根据全等三角形的判定证△DAM≌△DPN,推出DN=DM,求出∠MDN60度,即可得到答案.
点评:本题主要考查对平行四边形的性质,三角形的内角和定理,垂线,全等三角形的性质和判定,等边三角形的判定,平行线的性质,角平分线的性质,多边形的内角和定理等知识点的理解和掌握,能综合运用这些性质进行推理是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
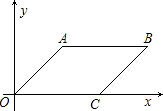 如图,在平行四边形ABC0中,已知点A、C两点的坐标为A(
如图,在平行四边形ABC0中,已知点A、C两点的坐标为A(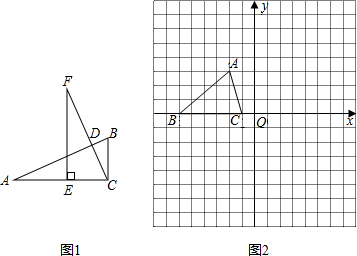
 (2013•南平模拟)如图,已知四边形ABCD.请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予证明.
(2013•南平模拟)如图,已知四边形ABCD.请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予证明.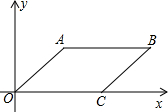 如图,在平行四边形OABC中,已知点A、C两点的坐标为A (
如图,在平行四边形OABC中,已知点A、C两点的坐标为A (