题目内容
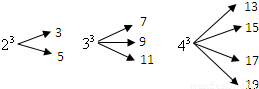
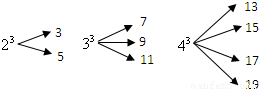
一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若63也按照此规律来进行“分裂”,则63“分裂”出的奇数中,最大的奇数是 .

【答案】分析:首先发现奇数的个数与前面的底数相同,再得出每一组分裂中的第一个数是底数×(底数-1)+1,问题得以解决.
解答:解:由23=3+5,分裂中的第一个数是:3=2×1+1,
33=7+9+11,分裂中的第一个数是:7=3×2+1,
43=13+15+17+19,分裂中的第一个数是:13=4×3+1,
53=21+23+25+27+29,分裂中的第一个数是:21=5×4+1,
63=31+33+35+37+39+41,分裂中的第一个数是:31=6×5+1,
所以63“分裂”出的奇数中最大的是6×5+1+2×(6-1)=41.
故答案为:41.
点评:本题是对数字变化规律的考查,找出分裂的第一个数的变化规律是解题的关键,也是求解的突破口.
解答:解:由23=3+5,分裂中的第一个数是:3=2×1+1,
33=7+9+11,分裂中的第一个数是:7=3×2+1,
43=13+15+17+19,分裂中的第一个数是:13=4×3+1,
53=21+23+25+27+29,分裂中的第一个数是:21=5×4+1,
63=31+33+35+37+39+41,分裂中的第一个数是:31=6×5+1,
所以63“分裂”出的奇数中最大的是6×5+1+2×(6-1)=41.
故答案为:41.
点评:本题是对数字变化规律的考查,找出分裂的第一个数的变化规律是解题的关键,也是求解的突破口.

练习册系列答案
相关题目
 (2012•菏泽)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若63也按照此规律来进行“分裂”,
(2012•菏泽)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若63也按照此规律来进行“分裂”, (2013•金平区模拟)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若73也按照此规律来进行“分裂”,则73“分裂”出的奇数中,最大的奇数是
(2013•金平区模拟)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若73也按照此规律来进行“分裂”,则73“分裂”出的奇数中,最大的奇数是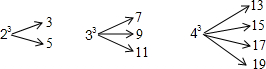
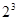 ,
,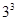 和
和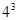 分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即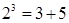 ;
;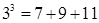 ;
;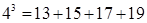 ;……;
;……;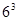 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则