题目内容
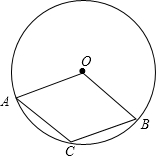如图，点A，C和B都在⊙O上，且四边形ACBO为菱形，求证：点C是 |
| AB |
考点：菱形的性质,圆心角、弧、弦的关系
专题：证明题
分析：根据菱形的性质以及圆心角、弧、弦的关系，得出
=
，进而得出答案．
|
| AC |
|
| BC |
解答：证明：∵点A，C和B都在⊙O上，且四边形ACBO为菱形，
∴AC=BC，
∴
=
，
∴点C是
的中点．
∴AC=BC，
∴
|
| AC |
|
| BC |
∴点C是
|
| AB |
点评：此题主要考查了菱形的性质以及同圆或等圆中圆心角、弧、弦的关系，得出AC=BC是解题关键．
练习册系列答案
相关题目
在梯形ABCD中，AD∥BC，∠B=90°，AB=12，BC=10，AD=5，则CD的长是（ ）
| A、13 | B、14 | C、15 | D、16 |
下列两个量的关系一定不是反比例关系的是（ ）
| A、若r为圆柱底面的半径，h为圆柱的高，当圆柱的侧面积一定时，h与r之间的关系 |
| B、汽车在一定路程上的行驶速度v（km/h）与行驶时间t（h）之间的关系 |
| C、三角形的面积一定，则三角形的高h与对应的底边长a之间的关系 |
| D、矩形的周长一定，其面积S与矩形的一边长x之间的关系 |
如图，已知在△ABC中，∠C=90°，AD是角平分线，过点B作BA的垂线与AD的延长线相交于点E，求证：△BDE是等腰三角形．
在4×4方格内画三角形ABC，使它的顶点在格点上，三条边长分别为2，2
解不等式组：