Question

【题目】如图，四边形ABCD内接于⊙O，AC⊥BD于点E，连按OA、OD，OA交BD于点F．

（1）如图1，求证：∠BAC=∠OAD；

（2）如图2，当AC=CD肘，求证：AB=BF；

（3）如图3，在（2）的条件下，当BD=11，AF=时．求OF的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）

【解析】试题分析：（1）如图1中，延长AO交⊙O于M，连接CM．只要证明CM∥BD，推出∠1=∠2，推出，推出∠BAC=∠DAO．
（2）由∠BAC=∠DAO，推出∠BAF=∠CAD，由CA=CD，所以∠CAD=∠CDA，由∠1=∠B，∠B+∠BAF+∠AFB=180°，∠1+∠CAD+∠ADC=180°，推出∠BAF=∠ADC=∠CAD=∠BAF，即可证明．
（3）如图3中，连接OB、DM．设BA=BF=x，⊙O的半径为r．由△ABF∽△AOB，推出，得x2=2r ①，由△ABF∽△DMF，推出，得x（11-x）=2（2r-2） ②，由①②解方程组即可解决问题．

试题解析：（1）证明：如图1中，延长AO交⊙O于M，连接CM．

∵AM是直径，
∴∠ACM=90°，
∵AC⊥BD，
∴∠AED=∠ACM=90°，
∴CM∥BD，
∴∠1=∠2，
∴，
∴∠BAC=∠DAO．
（2）证明：如图2中，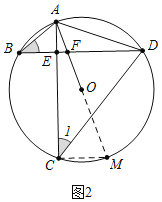

∵∠BAC=∠DAO，
∴∠BAF=∠CAD，
∵CA=CD，
∴∠CAD=∠CDA，
∵∠1=∠B，∠B+∠BAF+∠AFB=180°，∠1+∠CAD+∠ADC=180°，
∴∠BAF=∠ADC=∠CAD=∠BAF，
∴BA=BF．
（3）解：如图3中，连接OB、DM．设BA=BF=x，⊙O的半径为r．

∵OB=OA，
∴∠OAB=∠OBA=∠BAF，
∴△ABF∽△AOB，
∴，
∴x2=2r ①，
∵∠ABF=∠M，∠AFB=∠DFM，
∴△ABF∽△DMF，
∴，
∴x（11-x）=2（2r-2） ②，
由①②可得x=5，r=，
∴OF=r-AF=-2=．