题目内容
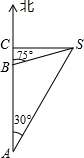 (2013•莒南县二模)如图,一渔船以32千米/时的速度向正北航行,在A处看到灯塔S在渔船的北偏东30°,半小时后航行到B处看到灯塔S在船的北偏东75°,若渔船继续向正北航行到C处时,灯塔S和船的距离最短,求灯塔S与C的距离.(计算过程和结果一律不取近似值)
(2013•莒南县二模)如图,一渔船以32千米/时的速度向正北航行,在A处看到灯塔S在渔船的北偏东30°,半小时后航行到B处看到灯塔S在船的北偏东75°,若渔船继续向正北航行到C处时,灯塔S和船的距离最短,求灯塔S与C的距离.(计算过程和结果一律不取近似值)(sin75°=
| ||||
| 4 |
分析:先过点B作BD⊥AS于点D,根据∠A=30°,求出BD的长,再根据∠BSA=∠CBS-∠A,求出∠BSA,最后根据SC=sin∠CBS×BS,代入计算即可.
解答:解:过点B作BD⊥AS于点D,
∵∠A=30°,AB=32×
=16(千米),
∴BD=8(千米),
∵∠BSA=∠CBS-∠A=75°-30°=45°,
∴BS=
=
=8
(千米),
∴SC=sin∠CBS×BS=sin75°×8
=
×8
=4
-4(千米);
答:灯塔S与C的距离是(4
-4)千米.
∵∠A=30°,AB=32×
| 1 |
| 2 |
∴BD=8(千米),
∵∠BSA=∠CBS-∠A=75°-30°=45°,
∴BS=
| BD |
| sin45° |
| 8 | ||||
|
| 2 |
∴SC=sin∠CBS×BS=sin75°×8
| 2 |
| ||||
| 4 |
| 2 |
| 3 |
答:灯塔S与C的距离是(4
| 3 |
点评:此题是一道方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
相关题目
 (2013•莒南县二模)如图,在⊙O中,OA、OB是半径,且OA⊥OB,OA=6,点C是AB上异于A、B的动点.过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点G、H在线段DE上,且DG=GH=HE.
(2013•莒南县二模)如图,在⊙O中,OA、OB是半径,且OA⊥OB,OA=6,点C是AB上异于A、B的动点.过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点G、H在线段DE上,且DG=GH=HE. (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: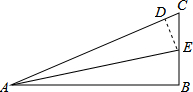 (2013•莒南县二模)如图所示的三角形纸片中,∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点D落在AC边上,折痕为AE,则BE的长为( )
(2013•莒南县二模)如图所示的三角形纸片中,∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点D落在AC边上,折痕为AE,则BE的长为( )