题目内容
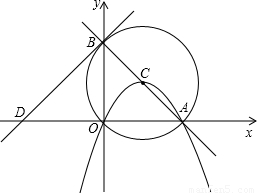
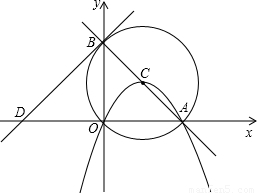
(2010•湘潭)如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)设四边形AFEC的面积为y,求y关于t的函数关系式,并求出y的最小值.
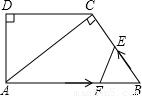
【答案】分析:(1)由CD∥AB,得∠DCA=∠CAB,加上一组直角,即可证得所求的三角形相似.
(2)在Rt△ABC中,由勾股定理可求得AC的长,根据(1)题所得相似三角形的比例线段,即可求出DC的长.
(3)分析图象可知:四边形AFEC的面积可由△ABC、△BEF的面积差求得,分别求出两者的面积,即可得到y、t的函数关系式,进而可根据函数的性质及自变量的取值范围求出y的最小值.
解答:解:(1)∵CD∥AB,∴∠BAC=∠DCA
又AC⊥BC,∠ACB=90°,∴∠D=∠ACB=90°,
∴△ACD∽△BAC.
(2)Rt△ABC中,AC=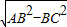 =8cm,
=8cm,
∵△ACD∽△BAC,∴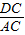 =
=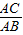 ,
,
即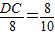 ,解得:DC=6.4cm.
,解得:DC=6.4cm.
(3)过点E作AB的垂线,垂足为G,
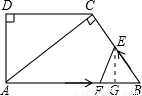 ∵∠ACB=∠EGB=90°,∠B公共,
∵∠ACB=∠EGB=90°,∠B公共,
∴△ACB∽△EGB,
∴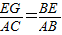 ,即
,即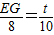 ,故
,故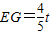 ;
;
y=S△ABC-S△BEF
=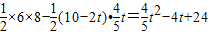
=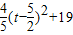 ;
;
故当t= 时,y的最小值为19.
时,y的最小值为19.
点评:此题考查了梯形的性质、相似三角形的判定和性质、图形面积的求法以及二次函数最值的应用等知识,能够将面积问题转换为二次函数的最值问题是解答(3)题的关键.
(2)在Rt△ABC中,由勾股定理可求得AC的长,根据(1)题所得相似三角形的比例线段,即可求出DC的长.
(3)分析图象可知:四边形AFEC的面积可由△ABC、△BEF的面积差求得,分别求出两者的面积,即可得到y、t的函数关系式,进而可根据函数的性质及自变量的取值范围求出y的最小值.
解答:解:(1)∵CD∥AB,∴∠BAC=∠DCA
又AC⊥BC,∠ACB=90°,∴∠D=∠ACB=90°,
∴△ACD∽△BAC.
(2)Rt△ABC中,AC=
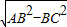 =8cm,
=8cm,∵△ACD∽△BAC,∴
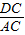 =
=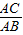 ,
,即
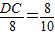 ,解得:DC=6.4cm.
,解得:DC=6.4cm.(3)过点E作AB的垂线,垂足为G,
 ∵∠ACB=∠EGB=90°,∠B公共,
∵∠ACB=∠EGB=90°,∠B公共,∴△ACB∽△EGB,
∴
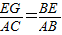 ,即
,即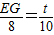 ,故
,故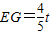 ;
;y=S△ABC-S△BEF
=
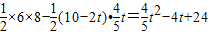
=
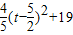 ;
;故当t=
 时,y的最小值为19.
时,y的最小值为19.点评:此题考查了梯形的性质、相似三角形的判定和性质、图形面积的求法以及二次函数最值的应用等知识,能够将面积问题转换为二次函数的最值问题是解答(3)题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目