题目内容
李明从厦门乘汽车沿高速公路前往A地,已知该汽车的平均速度是100千米/小时,它行驶t小时候距厦门的路程为S1千米.另有王红同时从A地乘汽车沿同一条高速公路回厦门,已知这辆汽车距厦门的路程S2(千米)与行驶时间t(时)之间的函数关系式为S2=kt+b(k、b为常数k≠0)
(1)若王红从A地回到厦门用了9小时,且当t=2时,S2=560.求k与b的值;
(2)试问在两辆汽车相遇之前,当行驶时间t的取值在什么范围内,两车的距离小于288千米?
解:(1))∵S2=kt+b,依题意得t=9时,S2=0,
又∵t=2时,S2=560
∴
解得: ;
;
(2)由题意得:S1=100t,
由(1)得,S2=-80t+720
令S1=S2,得100t=-80t+720,
解得t=4,
当t<4时,S2>S1,
∴S2-S1<288,
即(-80t+720)-100t<288,
-180t<-432
∴180t>32,
解得t>2.4,
∴在两车相遇之前,
当2.4<t<4时,两车的距离小于288千米.
分析:(1)把(9,0),(2,560)代入一次函数解析式可得k与b的值;
(2)先求得两车相遇时的时间,那么相遇前t<4,进而根据t<4时,王红距离厦门的路程远,让S2-S1<288列式求值即可.
点评:考查一次函数的应用;判断出两车距离少于288千米时所符合的不等式是解决本题的难点.
又∵t=2时,S2=560
∴

解得:
 ;
;(2)由题意得:S1=100t,
由(1)得,S2=-80t+720
令S1=S2,得100t=-80t+720,
解得t=4,
当t<4时,S2>S1,
∴S2-S1<288,
即(-80t+720)-100t<288,
-180t<-432
∴180t>32,
解得t>2.4,
∴在两车相遇之前,
当2.4<t<4时,两车的距离小于288千米.
分析:(1)把(9,0),(2,560)代入一次函数解析式可得k与b的值;
(2)先求得两车相遇时的时间,那么相遇前t<4,进而根据t<4时,王红距离厦门的路程远,让S2-S1<288列式求值即可.
点评:考查一次函数的应用;判断出两车距离少于288千米时所符合的不等式是解决本题的难点.

练习册系列答案
相关题目
3月份,学校举行了“艺术节”活动,九年级(1)班同学取得了优异的成绩.为了表彰获奖同学,班主任林老师特意到瑞安书城购买书籍作为奖品.瑞安书城二楼专设7.5折售书架,销售文教类图书,部分书籍和标价如下表:
| 书名 | 原价(元) |
| 中国历史故事 | 50 |
| 名人名言 | 20 |
| 文化苦旅 | 28 |
①经打7.5折后,购买《中国历史故事》的总价为________元(用含x的代数式表示),购买《名人名言》的总价为________元(用含y的代数式表示).
②若林老师购买《中国历史故事》和《名人名言》这两种书时,共付了480元钱,求这两种书各购买了多少本?
③设林老师购买《中国历史故事》和《名人名言》这两种书共付了w元,请求出w关于x的函数关系式;
(2)若林老师在书城购买了以上三种书共20本,恰好付了450元,则其中购买了《中国历史故事》________本.(请直接写出答案)



 如图,D,E分别是△ABC的边AC,BC的中点,则下列说法错误的是
如图,D,E分别是△ABC的边AC,BC的中点,则下列说法错误的是 ,4
,4 的大小(用小于符号连接)________.
的大小(用小于符号连接)________. 如图是某报记者在抽样调查了一些市民八小时以外用于读书的时间(单位:分钟)后,绘制的频率分布直方图,图中从左向右的前六个长方形的面积之和为0.95,200~230分钟这一组的频数是10,此次抽样的样本容量是
如图是某报记者在抽样调查了一些市民八小时以外用于读书的时间(单位:分钟)后,绘制的频率分布直方图,图中从左向右的前六个长方形的面积之和为0.95,200~230分钟这一组的频数是10,此次抽样的样本容量是


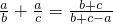 ,则三角形是
,则三角形是