题目内容
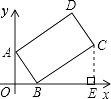
【题目】如图,矩形ABCD中,AB=2,BC=4,点A,B分别在y轴、x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标是 . 
【答案】(1+2 ![]() ,2)
,2)
【解析】解:∵AB=2,∠OAB=30°,
∴OB= ![]() AB=1,
AB=1,
在矩形ABCD中,∠ABC=90°,
∴∠OAB+∠ABO=90°,∠AB0+∠CBE=90°,
∴∠CBE=∠OAB=30°,
点C作CE⊥x轴于点E,
在Rt△BCE中,CE= ![]() BC=
BC= ![]() ×4=2,BE=
×4=2,BE= ![]() =
= ![]() =2
=2 ![]() ,
,
∴OE=OB+BE=1+2 ![]() ,
,
∴点C的坐标是(1+2 ![]() ,2).
,2).
故答案为:(1+2 ![]() ,2).
,2).
利用含30度角的直角三角形的性质得OB= 1,由矩形性质、同角的余角相等得∠CBE=∠OAB=30°从而得CE的长度,再利用勾股定理得BE的长度,从而得出C点的坐标。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?



