题目内容
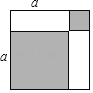
【题目】(1)仔细观察如图图形,利用面积关系写出一个等式:a2+b2= .
(2)根据(1)中的等式关系解决问题:已知m+n=4,mn=﹣2,求m2+n2的值.
(3)小明根据(1)中的关系式还解决了以下问题:
“已知m+![]() =3,求m2+
=3,求m2+![]() 和m3+
和m3+![]() 的值”
的值”
小明解法:
![]()
![]()
![]()
请你仔细理解小明的解法,继续完成:求m5+m﹣5的值
【答案】(1)(a+b)2﹣2ab;(2)20;(3)123
【解析】
(1)观察原式为阴影部分的面积,再用大矩形的面积减去两个空白矩形的面积也可表示阴影部分面积,进而得出答案;
(2)运用(1)中的结论进行计算便可把原式转化为(m+n)2﹣2mn进行计算;
(3)把原式转化为(m2+m﹣2)(m3+m﹣3)﹣(m+m﹣1)进行计算.
解:(1)根据图形可知,阴影部分面积为a2+b2,
阴影部分面积可能表示为(a+b)2﹣2ab,
∴a2+b2=(a+b)2﹣2ab,
故答案为:(a+b)2﹣2ab;
(2)m2+n2=(m+n)2﹣2mn=42﹣2×(﹣2)=20;
(3)m5+m﹣5=(m2+m﹣2)(m3+m﹣3)﹣(m+m﹣1)=7×18﹣3=123.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目