题目内容
C是线段AB的中点,D是线段CB上的一点,如图所示,若所有线段的长度都是正整数,且线段AB的所有可能的长度数的乘积等于140,则线段AB的所有可能的长度数的和等于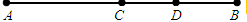
分析:根据题意和图形,先判断出CD、BD的长度,再由BC=CD+BD=
≥2,判断出AB为不小于4的偶数,从而得出AB可能的最小三个偶数为4,6,8,乘积>140,最后得出AB只有2种可能,即140分解为2个偶数的乘积:10*14=140,继而得出答案.
| AB |
| 2 |
解答:解:如果若所有线段的长度都是正整数,则:
CD≥1
BD≥1
BC=CD+BD=
≥2,AB≥4,AB为不小于4的偶数
AB可能的最小三个偶数为4,6,8,乘积>140
所以AB只有2种可能,即140分解为2个偶数的乘积:10*14=140
即AB长度的可能为10或14,可能的长度数的和为24.
故答案为24.
CD≥1
BD≥1
BC=CD+BD=
| AB |
| 2 |
AB可能的最小三个偶数为4,6,8,乘积>140
所以AB只有2种可能,即140分解为2个偶数的乘积:10*14=140
即AB长度的可能为10或14,可能的长度数的和为24.
故答案为24.
点评:本题考查了质因数分解问题,解题的关键是结合图形,求出AB的长度范围,从而AB长度的可能,此题难度较大.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
线段AB长为8cm,点C是线段AB的中点,点D是线段AC的中点,则线段BD的长为( )
| A、2cm | B、4cm | C、6cm | D、8cm |
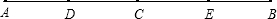
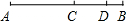 如图,点C是线段AB的中点,AB=6cm,如果点D是线段AB上一点,且BD=1cm,那么CD=
如图,点C是线段AB的中点,AB=6cm,如果点D是线段AB上一点,且BD=1cm,那么CD=
