题目内容
【题目】如图,点![]() 在函数
在函数![]() 的图象上,直线
的图象上,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,且点
,且点![]() 的横坐标为4,点
的横坐标为4,点![]() 的纵坐标为
的纵坐标为![]() ,则
,则![]() 的面积是________.
的面积是________.

【答案】![]()
【解析】
作EC⊥x轴于C,EP⊥y轴于P,FD⊥x轴于D,FH⊥y轴于H,由题意可得点A,B的坐标分别为(4,0),B(0,![]() ),利用待定系数法求出直线AB的解析式,再联立反比例函数解析式求出点,F的坐标.由于S△OEF+S△OFD=S△OEC+S梯形ECDF,S△OFD=S△OEC=1,所以S△OEF=S梯形ECDF,然后根据梯形面积公式计算即可.
),利用待定系数法求出直线AB的解析式,再联立反比例函数解析式求出点,F的坐标.由于S△OEF+S△OFD=S△OEC+S梯形ECDF,S△OFD=S△OEC=1,所以S△OEF=S梯形ECDF,然后根据梯形面积公式计算即可.
解:如图,作EP⊥y轴于P,EC⊥x轴于C,FD⊥x轴于D,FH⊥y轴于H,
由题意可得点A,B的坐标分别为(4,0),B(0,![]() ),
),
由点B的坐标为(0,![]() ),设直线AB的解析式为y=kx+
),设直线AB的解析式为y=kx+![]() ,将点A的坐标代入得,0=4k+
,将点A的坐标代入得,0=4k+![]() ,解得k=-
,解得k=-![]() .
.
∴直线AB的解析式为y=-![]() x+
x+![]() .
.
联立一次函数与反比例函数解析式得,
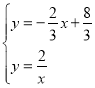 ,解得
,解得![]() 或
或![]() ,
,
即点E的坐标为(1,2),点F的坐标为(3,![]() ).
).
∵S△OEF+S△OFD=S△OEC+S梯形ECDF,而S△OFD=S△OEC=![]() ×2=1,
×2=1,
∴S△OEF=S梯形ECDF=![]() ×(AF+CE)×CD=
×(AF+CE)×CD=![]() ×(
×(![]() +2)×(3-1)=
+2)×(3-1)=![]() .
.
故答案为:![]() .
.


练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目