题目内容
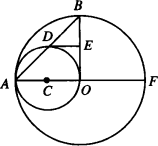
如图,AF是⊙O的直径,以OA为直径的⊙C与⊙O的弦AB相交于点D,DE⊥OB,垂足为E.求证:DE是⊙C的切线.
答案:
解析:
解析:
|
证明:连接CD,在△AOB中,因为AO=OB,所以∠OBA=∠OAB. 在△ACD中,AC=CD,∠OAB=∠CDA,所以∠OBA=∠CDA. 所以CD∥OB即CD∥OE,所以CD⊥DE,所以DE是⊙C的切线. |

练习册系列答案
相关题目
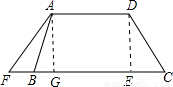
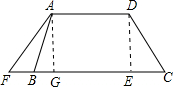 度DE与水平宽度CE的比),CD的长为10m,天桥另一斜面AB的坡角∠ABG=45°
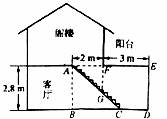
度DE与水平宽度CE的比),CD的长为10m,天桥另一斜面AB的坡角∠ABG=45° 汪老师要装修自己带阁楼的新居(如图为新居剖面图),在建造客厅到阁楼的楼梯AC时,为避免上楼时墙角F碰头,设计墙角F到楼梯的竖直距离FG为1.75m.他量得客厅高AB=2.8m,楼梯洞口宽AF=2m,阁楼阳台宽EF=3m.要使墙角F到楼梯的竖直距离FG为1.75m,楼梯底端C到墙角D的距离CD是
汪老师要装修自己带阁楼的新居(如图为新居剖面图),在建造客厅到阁楼的楼梯AC时,为避免上楼时墙角F碰头,设计墙角F到楼梯的竖直距离FG为1.75m.他量得客厅高AB=2.8m,楼梯洞口宽AF=2m,阁楼阳台宽EF=3m.要使墙角F到楼梯的竖直距离FG为1.75m,楼梯底端C到墙角D的距离CD是 (i=1:
(i=1: 是指铅直高度DE与水平宽度CE的比),CD的长为10cm,天桥另一斜面AB的坡角∠ABG=45°。
是指铅直高度DE与水平宽度CE的比),CD的长为10cm,天桥另一斜面AB的坡角∠ABG=45°。
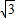 (i=1:
(i=1: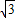 是指铅直高度DE与水平宽度CE的比),CD的长为10m,天桥另一斜面AB的坡角∠ABG=45°
是指铅直高度DE与水平宽度CE的比),CD的长为10m,天桥另一斜面AB的坡角∠ABG=45°