题目内容
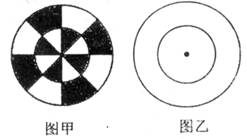
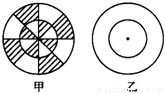
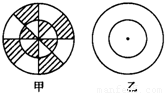
小明与小华在玩一个掷飞镖游戏,如图甲是一个把两个同心圆平均分成8份的靶,当飞镖掷中阴影部分时,小明胜,否则小华胜(没有掷中靶或掷到边界线时重掷).(1)不考虑其他因素,你认为这个游戏公平吗?说明理由;
(2)请你在图乙中,设计一个不同于图甲的方案,使游戏双方公平.

【答案】分析:本题考查概率问题中的公平性问题,解决本题的关键是计算出各种情况的概率,然后比较即可.
解答:解:(1)这个游戏公平.(2分)
∵根据图甲的对称性,阴影部分的面积等于圆面积的一半,
∴这个游戏公平.(4分)
(2)把图乙中的同心圆平均分成偶数等分,如图,当飞镖掷中奇数时小明胜,掷中偶数时小华胜.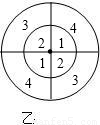
点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个参与者取胜的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.
解答:解:(1)这个游戏公平.(2分)
∵根据图甲的对称性,阴影部分的面积等于圆面积的一半,
∴这个游戏公平.(4分)
(2)把图乙中的同心圆平均分成偶数等分,如图,当飞镖掷中奇数时小明胜,掷中偶数时小华胜.

点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个参与者取胜的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 16、小明与小华在玩一个掷飞镖游戏,如图甲是一个把两个同心圆平均分成8份的靶,当飞镖掷中阴影部分时,小明胜,否则小华胜(没有掷中靶或掷到边界线时重掷).
16、小明与小华在玩一个掷飞镖游戏,如图甲是一个把两个同心圆平均分成8份的靶,当飞镖掷中阴影部分时,小明胜,否则小华胜(没有掷中靶或掷到边界线时重掷).