题目内容
已知两圆的半径恰为方程2x2-5x+2=0的两根，圆心距为
，则这两个圆的外公切线有（ ）条．
| 3 |
| A、0 | B、1 | C、2 | D、3 |
分析：首先解一元二次方程求得两圆的半径，再根据数量关系判断两圆的位置关系，进一步确定其外公切线的条数．
解答：解：解方程2x2-5x+2=0，得
两圆的半径是2和
，显然2-
＜
＜2+
，
则两圆相交，即这两个圆的外公切线有2条．
故选C．
两圆的半径是2和
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
则两圆相交，即这两个圆的外公切线有2条．
故选C．
点评：此题考查了一元二次方程的解法、两圆的位置关系与数量之间的联系以及外公切线的条数，综合性较强．
练习册系列答案
阅读快车系列答案
相关题目
已知两圆的半径恰为方程2x2-5x+2=0的两根，圆心距为2
，则这两个圆的外公切线有（ ）
| 3 |
| A、0条 | B、1条 | C、2条 | D、3条 |
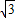，则这两个圆的外公切线有（ ）
，则这两个圆的外公切线有（ ）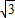
，则这两个圆的外公切线有（ ）