题目内容
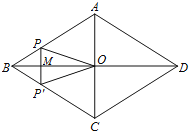
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
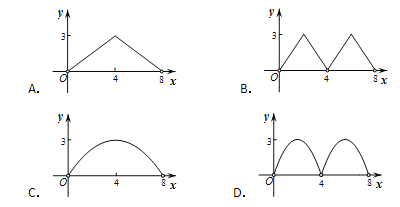
【答案】D
【解析】
试题分析:由菱形的性质得出AB=BC=CD=DA,OA=![]() AC=3,OB=
AC=3,OB=![]() BD=4,AC⊥BD,分两种情况:
BD=4,AC⊥BD,分两种情况:
①当BM≤4时,先证明△P′BP∽△CBA,得出比例式![]() ,求出PP′,得出△OPP′的面积y是关于x的二次函数,即可得出图象的情形;
,求出PP′,得出△OPP′的面积y是关于x的二次函数,即可得出图象的情形;
②当BM≥4时,y与x之间的函数图象的形状与①中的相同;即可得出结论.
解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,OA=![]() AC=3,OB=
AC=3,OB=![]() BD=4,AC⊥BD,
BD=4,AC⊥BD,
①当BM≤4时,
∵点P′与点P关于BD对称,
∴P′P⊥BD,
∴P′P∥AC,
∴△P′BP∽△CBA,
∴![]() ,即
,即![]() ,
,
∴PP′=![]() x,
x,
∵OM=4﹣x,
∴△OPP′的面积y=![]() PP′×OM=
PP′×OM=![]() ×
×![]() x(4﹣x)=﹣
x(4﹣x)=﹣![]() x2+3x;
x2+3x;
∴y与x之间的函数图象是抛物线,开口向下,过(0,0)和(4,0);
②当BM≥4时,y与x之间的函数图象的形状与①中的相同,过(4,0)和(8,0);
综上所述:y与x之间的函数图象大致为
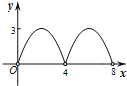 .
.
故选:D.

练习册系列答案
相关题目
