题目内容
【题目】如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点,若∠APB=40°,PA=5,则下列结论:①PA=PB=5;②△PCD的周长为5;③∠COD=70°.正确的个数为( )
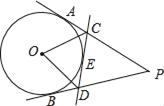
A. 3个 B. 2个 C. 1个 D. 0个
【答案】B
【解析】
根据切线长定理,可判断①正确;将△PCD的周长转化为PA+PB,可判断②错误;连接OA、OB、OE,求出∠AOB,再由∠COD=∠COE+∠EOD=![]() (∠AOE+∠BOE)=
(∠AOE+∠BOE)=![]() ∠AOB,可判断③正确;
∠AOB,可判断③正确;
解:∵PA、PB是⊙O的切线,
∴PA=PB,故①正确;
∵PA、PB、CD是⊙O的切线,
∴CA=CE,DE=DB,
∴△PCD的周长=PC+CE+DE+PD=PC+CA+PD+DB=PA+PB=2PA=10,故②错误;
连接OA、OB、OE,
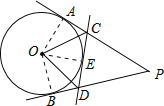
∠AOB=180°-∠APB=140°,
∴∠COD=∠COE+∠EOD=![]() (∠AOE+∠BOE)=
(∠AOE+∠BOE)=![]() ∠AOB=70°,故③正确.
∠AOB=70°,故③正确.
综上可得①③正确,共2个.
故选B.

练习册系列答案
相关题目